
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,且点
,且点![]() 的横坐标为
的横坐标为![]() .
.
(1)请用![]() 的代数式表示
的代数式表示![]() ;
;
(2)点![]() 在直线
在直线![]() 上,点
上,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
①若抛物线![]() 过点
过点![]() ,求该抛物线的解析式;
,求该抛物线的解析式;
②若抛物线![]() 与线段
与线段![]() 恰有一个交点,直接写出
恰有一个交点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)把x=-2代入直线l的解析式求得![]() ,再把
,再把![]() 代入抛物线的解析式即可得
代入抛物线的解析式即可得![]() ;
;
(2)①把x=-1代入直线l的解析式求得![]() ,再根据待定系数法求出抛物线解析式即可;②先根据题意求得
,再根据待定系数法求出抛物线解析式即可;②先根据题意求得![]() 或
或![]() ,再分情况:1)当抛物线顶点在线段BC上时,2)当抛物线与线段BC有一个交点时,分别求解即可.
,再分情况:1)当抛物线顶点在线段BC上时,2)当抛物线与线段BC有一个交点时,分别求解即可.
(1)把x=-2代入直线l的解析式得
![]()
∴![]()
把![]() 代入抛物线的解析式得
代入抛物线的解析式得
![]()
解得![]() ;
;
(2)①把x=-1代入直线l的解析式得
![]()
∴![]()
把![]() 代入抛物线的解析式得
代入抛物线的解析式得
![]()
解得![]()
∴![]()
∴![]() ;
;
②∵![]()
∴对称轴x=b开口向下,顶点为![]()
当抛物线M与线段BC恰有一个交点时,交点纵坐标为5,此时![]()
整理得![]()
∵![]()
∴![]()
解得![]() 或
或![]()
当抛物线顶点在线段BC上时,如图
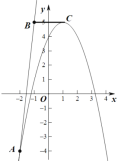 或
或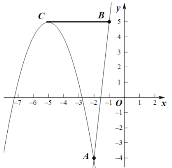
当![]() 时,抛物线与线段BC恰有一个交点
时,抛物线与线段BC恰有一个交点
解得b=1或b=-5,此时顶点为![]() 或
或![]()
当抛物线与线段BC有一个交点时,如图
 或
或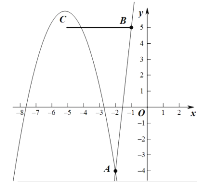
如上左图中,此时交点为![]() 应在点
应在点![]() 右侧即
右侧即![]()
解得![]() ,
,![]() 或
或![]() (舍去)与最初取值矛盾
(舍去)与最初取值矛盾
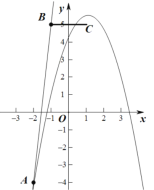
如上右图中,此时交点为![]() ,应在点
,应在点![]() 的右侧即
的右侧即![]()
解得![]() 或
或![]()
故抛物线与线段BC恰有一个交点时,![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最小值为( )
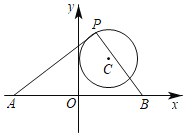
A.4B.3C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
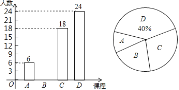
【题目】为深化课程改革,提高学生的综合素质,我校开设了形式多样的校本课程.为了解校本课程在学生中最受欢迎的程度,学校随机抽取了部分学生进行调查,从A:天文地理;B:科学探究;C:文史天地;D:趣味数学;四门课程中选你喜欢的课程(被调查者限选一项),并将调查结果绘制成两个不完整的统计图,如图所示,根据以上信息,解答下列问题:
(1)本次调查的总人数为 人,扇形统计图中A部分的圆心角是 度;
(2)请补全条形统计图;
(3)根据本次调查,该校400名学生中,估计最喜欢“科学探究”的学生人数为多少?
(4)为激发学生的学习热情,学校决定举办学生综合素质大赛,采取“双人同行,合作共进”小组赛形式,比赛题目从上面四个类型的校本课程中产生,并且规定:同一小组的两名同学的题目类型不能相同,且每人只能抽取一次,小琳和小金组成了一组,求他们抽到“天文地理”和“趣味数学”类题目的概率是多少?(请用画树状图或列表的方法求)
查看答案和解析>>
科目:初中数学 来源: 题型:
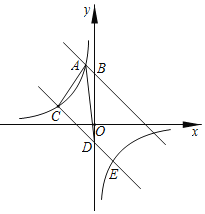
【题目】如图,在平面直角坐标系中,直线AB与y轴交于点![]() ,与反比例函数
,与反比例函数![]() 在第二象限内的图象相交于点
在第二象限内的图象相交于点![]() .
.
(1)求直线AB的解析式;
(2)将直线AB向下平移9个单位后与反比例函数的图象交于点C和点E,与y轴交于点D,求![]() 的面积;
的面积;
(3)设直线CD的解析式为![]() ,根据图象直接写出不等式
,根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈69中学为了组织一次球类对抗赛,在本校随机抽取了若干名学生,对他们每人最喜欢的一项球类运动进行了统计,将调查结果整理后绘制成如图所示的不完整的统计图.
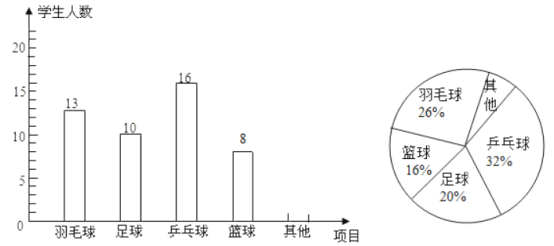
请你根据以上信息回答下列问题:
(1)求本次被调查的学生人数;
(2)通过计算补全条形统计图;
(3)若全校有4500名学生,请你估计该校最喜欢篮球运动的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”,图①是由边长![]() 的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为_______
的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为_______![]() (结果保留根号).
(结果保留根号).
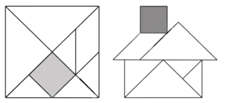
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于![]() ,点D是
,点D是![]() 的中点,且与点C位于AB的异侧,CD交AB于点E.
的中点,且与点C位于AB的异侧,CD交AB于点E.
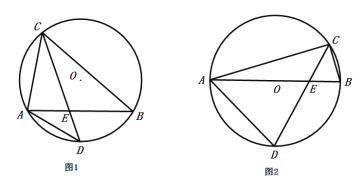
(1)求证:△ADE∽△CDA
(2)如图2,若![]() 的直径AB
的直径AB![]() ,CE=2,求AD和CD的长.
,CE=2,求AD和CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com