
【题目】已知直线AB:y=kx+b经过点B(1,4)、A(5,0)两点,且与直线y=2x-4交于点C.
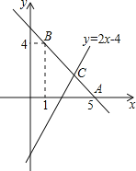
(1)求直线AB的解析式并求出点C的坐标;
(2)求出直线y=kx+b、直线y=2x-4及与y轴所围成的三角形面积;
(3)现有一点P在直线AB上,过点P作PQ∥y轴交直线y=2x-4于点Q,若线段PQ的长为3,求点P的坐标.
【答案】(1)y=-x+5;点C(3,2);(2)S=![]() ;(3)P点坐标为(2,3)或(4,1).
;(3)P点坐标为(2,3)或(4,1).
【解析】
(1)根据待定系数法求出直线AB解析式,再联立两函数解出C点坐标;
(2)依次求出y=-x+5和y=2x-4与y轴交点坐标,根据三角形的面积公式即可求解;
(3)设P点(m,-m+5) Q点坐标为(m,2m-4),根据线段PQ的长为3,分情况即可求解.
(1)∵直线y=kx+b经过点A(5,0),B(1,4),
∴ ![]()
解得 ![]()
∴直线AB的解析式为:y=-x+5;
∵若直线y=2x-4与直线AB相交于点C,
∴![]()
解得![]()
∴点C(3,2);
(2)∵y=-x+5与y轴交点坐标为(0,5),y=2x-4与y轴交点坐标为(0,-4)
,C点坐标为(3,2)
∴S=![]()
(3)设P点(m,-m+5) Q点坐标为(m,2m-4)
则-m+5-(2m-4)=3 或者2m-4-(-m+5)=3
解得m= 2 或m=4
∴P点坐标为(2,3)或(4,1).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交于点H,连接BD、FH.
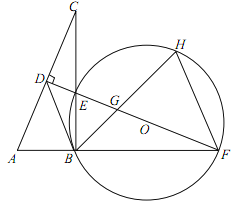
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并回答问题.事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方,这个结论就是著名的勾股定理.请利用这个结论,完成下面活动:
![]() 一个直角三角形的两条直角边分别为
一个直角三角形的两条直角边分别为![]() ,那么这个直角三角形斜边长为____;
,那么这个直角三角形斜边长为____;
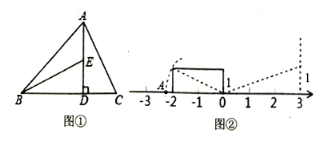
![]() 如图①,
如图①,![]() 于
于![]() ,求
,求![]() 的长度;
的长度;
![]() 如图②,点
如图②,点![]() 在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数
在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数![]() 的
的![]() 点(保留痕迹).
点(保留痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三明射击队员在某次训练中的成绩如下表:
队员 | 成绩(单位:环) | |||||||||
甲 | 6 | 6 | 7 | 7 | 8 | 9 | 9 | 9 | 9 | 10 |
乙 | 6 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 10 |
丙 | 6 | 6 | 6 | 7 | 7 | 8 | 10 | 10 | 10 | 10 |
针对上述成绩,三位教练是这样评价的:
教练![]() :三名队员的水平相当;
:三名队员的水平相当;
教练![]() :三名队员每人都有自己的优势;
:三名队员每人都有自己的优势;
教练![]() :如果从不同的角度分析,教练
:如果从不同的角度分析,教练![]() 和
和![]() 说的都有道理.
说的都有道理.
你同意教练![]() 的观点吗?通过数据分析,说明你的理由.
的观点吗?通过数据分析,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
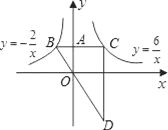
【题目】如图,在平面直角坐标系中,A为y轴正半轴上一点,过点A作x轴的平行线,交函数![]() 的图象于B点,交函数
的图象于B点,交函数![]() 的图象于C,过C作y轴和平行线交BO的延长线于D.
的图象于C,过C作y轴和平行线交BO的延长线于D.
(1)如果点A的坐标为(0,2),求线段AB与线段CA的长度之比;
(2)如果点A的坐标为(0,a),求线段AB与线段CA的长度之比;
(3)在(1)条件下,四边形AODC的面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=﹣2x+b的图象交x轴于点A、与正比例函数y2=2x的图象交于点M(m,m+2),
(1)求点M坐标;
(2)求b值;
(3)点O为坐标原点,试确定△AOM的形状,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘广告策划人员一名,对甲、乙、丙三名候选人进行三项素质测试,他们的各项测试成绩如下表所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
创新 | 72 | 85 | 67 |
综合知识 | 50 | 74 | 70 |
语言 | 88 | 45 | 67 |
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按5:3:2的比例确定各人的测试成绩,此时谁将被录用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com