
| 大桥名称 | 跨海大桥1 | 跨海大桥2 |
| 大桥长度 | 48千米 | 36千米 |
| 过桥费 | 100元 | 80元 |
分析 (1)根据往返的时间、速度和路程可得到一个一元一次方程,解此方程可得A与B两地间的高速公路路程;
(2)根据表格和王老师从A到B所花的高速公路通行费可以将解析式y=ax+b+5转换成一个含有未知数a的一元一次方程,解此方程可得轿车的高速公路里程费.
解答 解:(1)设A与B两地间的高速公路路程为s千米,由题意得,
$\frac{s}{4}$-$\frac{s}{4.5}$=10.
4.5s-4s=180,
0.5s=180,
解得s=360,
所以A与B两地间的高速公路路程为:360千米;
(2)轿车的高速公路通行费y(元)的计算方法为:y=ax+b+5,
根据表格和王老师的通行费可知,
y=295.4,x=360-48-36=276,b=100+80=180,将它们代入y=ax+b+5中得,
295.4=276a+180+5,
解得a=0.4,
所以轿车的高速公路里程费为:0.4元/千米.
点评 本题考查的是用一元一次方程解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求值时,关键是应用一次函数的性质;即由函数y随x的变化,确定取值.


科目:初中数学 来源: 题型:解答题
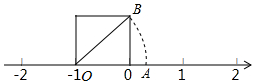 如图所示,认真观察,探讨下列问题:
如图所示,认真观察,探讨下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
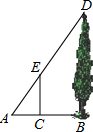 已知如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为 1.6m,并测得BC=2.2m,CA=0.8m,那么树DB的高度是( )
已知如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为 1.6m,并测得BC=2.2m,CA=0.8m,那么树DB的高度是( )| A. | 6m | B. | 5.6m | C. | 5.4m | D. | 4.4m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
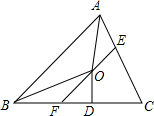 如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:| A. | ①② | B. | ③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com