
【题目】某学校初一、初二年级各有500名学生,为了解两个年级的学生对消防安全知识的掌握情况,学校从初一、初二年级各随机抽取20名学生进行消防安全知识测试,满分100分,成绩整理分析过程如下,请补充完整:
(收集数据)
初一年级20名学生测试成绩统计如下:
78 56 74 81 95 75 87 70 75 90 75 79 86 60 54 80 66 69 83 97
初二年级20名学生测试成绩不低于80,但是低于90分的成绩如下:
83 86 81 87 80 81 82
(整理数据)按照如下分数段整理、描述两组样本数据:
成绩 |
|
|
|
|
|
初一 | 2 | 3 | 7 | 5 | 3 |
初二 | 0 | 4 | 5 | 7 | 4 |
(分析数据)两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
初一 | 76.5 | 76.5 |
| 132.5 |
初二 | 79.2 |
| 74 | 100.4 |
(1)直接写出![]() ,
,![]() 的值;
的值;
(2)根据抽样调查数据,估计初一年级消防安全知识测试成绩在70分及其以上的大约有多少人?
(3)通过以上分析,你认为哪个年级对消防安全知识掌握得更好,并说明推断的合理性.
【答案】(1)![]() ,
,![]() ;(2)375;(3)初二年级对消防安全知识掌握得更好,理由详见解析
;(2)375;(3)初二年级对消防安全知识掌握得更好,理由详见解析
【解析】
(1)根据初二学生抽取20人,则中位数是20个成绩排序后第10与第11的平均数,将数据从小到大排列,根据表格知,第10与第11名的成绩在80至90分段里,确定即可;初一数据中超出出现次数最多的数据,即为众数;
(2)先计算初一样本超过70分的百分比,用样本估计总体,即可估计出初一年级测试成绩在70分及其以上的人数;
(3)综合比较平均数,中位数,众数,方差,进行说明即可.
解:(1)初二一共抽取20人进行测试,则中位数是20个成绩排序后第10与第11的平均数,将数据从小到大排列,根据表格知,第10与第11名的成绩在80至90分段里,且第10名为80分,第11名为81分,因此![]() ;
;
分析初一测试成绩知,众数为75,因此![]() .
.
故答案为:![]() ,
,![]()
(2)根据初一抽样调查数据,样本中成绩在70分及以上的比例为![]() ,因此估计初一年级测试成绩在70分及以上的人数有
,因此估计初一年级测试成绩在70分及以上的人数有![]()
答:估计初一年级测试成绩在70分及以上的人数有375人
(3)答:初二年级对消防安全知识掌握得更好,
理由如下:
①初二年级测试成绩的平均分相较于初一年级更高,说明初二年级的整体掌握情况更好;
②初二年级测试成绩的方差相较于初一年级更高,说明初二年级的掌握情况更稳定;
③初二年级测试成绩的中位数相较于初一年级更高,说明初二年级测试成绩的高分更多,掌握得很好的人数更多.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,CD平分∠ACB,点D,E关于CB对称,连接EB并延长,与AD的延长线交于点F,连接DE,CE.对于以下结论:
①DE垂直平分CB;②AD=BE;③∠F不一定是直角;④EF2+DF2=2CD2.
其中正确的是( )
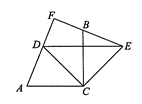
A.①④B.②③C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx﹣5的图象与x轴交于A、B两点,与y轴交于点C,其中点A坐标为(﹣1,0),一次函数y=x+k的图象经过点B、C.
(1)试求二次函数及一次函数的解析式;
(2)如图1,点D(2,0)为x轴上一点,P为抛物线上的动点,过点P、D作直线PD交线段CB于点Q,连接PC、DC,若S△CPD=3S△CQD,求点P的坐标;
(3)如图2,点E为抛物线位于直线BC下方图象上的一个动点,过点E作直线EG⊥x轴于点G,交直线BC于点F,当EF+![]() CF的值最大时,求点E的坐标.
CF的值最大时,求点E的坐标.
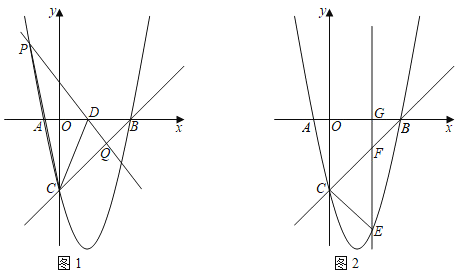
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.
有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.
(1)①方程![]() 半等分根方程(填“是”或“不是”);
半等分根方程(填“是”或“不是”);
②若![]() 是半等分根方程,则代数式
是半等分根方程,则代数式![]() ;
;
(2)若点![]() 在反比例函数
在反比例函数![]() 的图象上,则关于
的图象上,则关于![]() 的方程
的方程![]() 是半等分根方程吗?并说明理由;
是半等分根方程吗?并说明理由;
(3)如果方程![]() 是半等分根方程,且相异两点
是半等分根方程,且相异两点![]() ,
,![]() 都在抛物线
都在抛物线![]() 上,试说明方程
上,试说明方程![]() 的一个根为
的一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为![]() .
.
(1)根据题意,填写下表:
单人间的房间数 | 10 | … |
| … | 30 |
双人间的房间数 | _________ | … |
| … | 60 |
三人间的房间数 | 70 | … | _________ | … | _________ |
养老床位数 | 260 | … | _________ | … | _________ |
(2)若该养老中心建成后可提供养老床位200个,求![]() 的值;
的值;
(3)求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x kg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元, y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
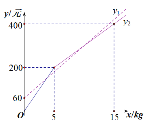
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5 kg后,超过的部分价格优惠是打五折
D.若顾客采摘12 kg草莓,那么到甲园或乙园的总费用相同
查看答案和解析>>
科目:初中数学 来源: 题型:
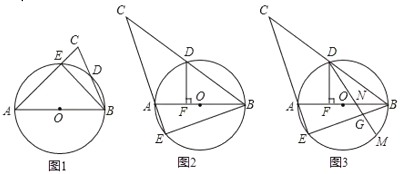
【题目】如图,在![]() 中,以
中,以![]() 为直径的
为直径的![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,
如图2,![]() 为钝角时,过点
为钝角时,过点![]() 作
作![]() 于点
于点![]() 求证:
求证:![]() ;
;
![]() 如图3,在
如图3,在![]() 的条件下,在∠BDF的内部作
的条件下,在∠BDF的内部作![]() ,使
,使![]() 分别交
分别交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com