
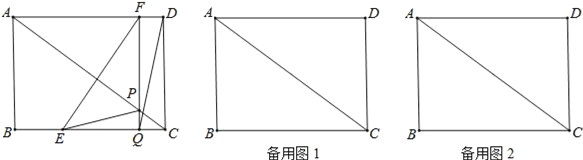
����Ŀ����ͼ���ھ���ABCD�У�AB=6cm��BC=8cm�������E�ɵ�B������BC�������C�����˶���ͬʱ��F�ɵ�D������DA�������A�����˶������ǵ��ٶȷֱ�Ϊ2cm/s��1cm/s��FQ��BC���ֱ�AC��BC�ڵ�P��Q�����˶�ʱ��Ϊt��s����0��t��4����
��1������EF��DQ�����ı���EQDFΪƽ���ı��Σ���t��ֵ��
��2������EP�����EPC�����Ϊycm2����y��t�ĺ�����ϵʽ������y�����ֵ��
��3������EPQ���ADC���ƣ���ֱ��д��t��ֵ��
���𰸡���1��t=2s����2��![]() ��3����3��2s��
��3����3��2s��![]() s��
s��![]() s��
s��
�����������������������ADC=��BCD=90����FQ��BC�ó��ı���FQCDΪ���Σ���CQ=DF=t��EQ=BC��BE=8��3t������ƽ���ı��ε����ʵã���t��ֵ������Rt��ABC�����ACB������ֵ��Ȼ���Rt��PQC����ACB������ֵ�ó�PQ�ij��ȣ�Ȼ��ó�y��t�ĺ�����ϵ�죬�����ֵ���������������Ƶó�t��ֵ��
�����������1���ھ���ABCD�У���ADC=��BCD=90������FQ��BC�����FQC=90�������ı���FQCDΪ���Σ�
��CQ=DF=t����EQ=BC-BE-CQ=8-2t-t=8-3t�� ���ı���EQDFΪƽ���ı��Σ� ��EQ=DF��
��t=8-3t�� ��t=2��s����
��2����Rt��ABC��tan��ACB=![]() �� ����Rt��PQC��tan��ACB=
�� ����Rt��PQC��tan��ACB=![]() �� ��PQ=
�� ��PQ=![]() ��
��
��![]() �� ��
�� ��![]() ����
����![]() �� ��y�����ֵΪ3��
�� ��y�����ֵΪ3��
��3������EPQ����ADC���ƣ�t��ֵΪ2s��![]() s��
s��![]() s��
s��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֵ20Ԫ��ֽ�һ���1Ԫ��5Ԫ��ֽ�ң������� ( )
A.4��B.5��C.6��D.7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.��3�ǩ�9��ƽ����
B.3�ǣ���3��2������ƽ����
C.����2��2��ƽ������2
D.8���������ǡ�2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.2x+3y=5xy
B.��m+3��2=m2+9
C.��xy2��3=xy6
D.a10��a5=a5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P����3����2���ڣ� ��
A.��һ����
B.�ڶ�����
C.��������
D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м����壺���ڳ����壻��Բ������Բ���������壬��һ��ƽ��ȥ������ļ����壬�����ܽس�Բ�ļ������У� ��
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com