
分析 分两种情况讨论:①第三边作为斜边;②第三边作为直角边;设出第三边的长,利用勾股定理列出方程解之即可.
解答 解:设第三条线段长为x.
①若第三条线段是斜边,则:
152+252=x2,
解得:x=$5\sqrt{34}$,
S=$\frac{1}{2}×15×25$=$\frac{375}{2}$;
②若第三条线段是直角边,则:
152+x2=252,
解得:x=20,
S=$\frac{1}{2}×15×20$=150.
故答案为:$5\sqrt{34}$或20;$\frac{375}{2}$或150.
点评 本题考查勾股定理的基本计算,难度不大.清楚勾股定理的基本内容是解答的关键.要特别注意的是,在题目没告诉哪条边是斜边的情况下,一定要分类讨论,不然就要漏解.


科目:初中数学 来源: 题型:选择题
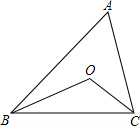 如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 115° | B. | 110° | C. | 105° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
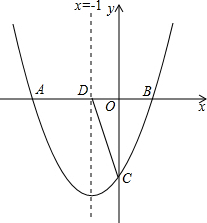 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴交点为A、B两点.其中点A 的坐标为(-3,0)
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴交点为A、B两点.其中点A 的坐标为(-3,0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
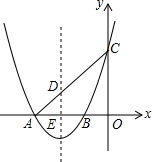 如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C.
如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com