
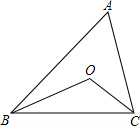
 如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 115° | B. | 110° | C. | 105° | D. | 130° |
分析 求出∠ABC+∠ACB的度数,根据角平分线的定义得出∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,求出∠OBC+∠OCB的度数,根据三角形内角和定理求出即可.
解答 解:∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°,
故选A.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.
五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
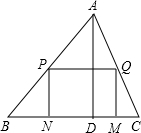 一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
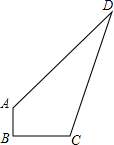 某开发区有一空地ABCD,如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,AD=13m,CD=12m,若每种植1平方米草皮需要150元,问总共需要投入多少元?
某开发区有一空地ABCD,如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,AD=13m,CD=12m,若每种植1平方米草皮需要150元,问总共需要投入多少元?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
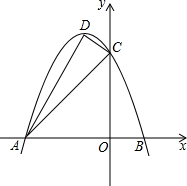 已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.
已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com