
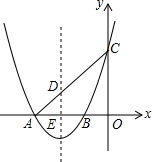
 如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C.
如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C. 分析 (1)令x=0,求出y,可得C点坐标;将抛物线解析式改写成交点式,可得A、B两点的坐标;
(2)将抛物线解析式配成顶点式;
(3)设出F点的横坐标,纵坐标用横坐标表示,将三角形ABF的面积用F点的横坐标表示出来,等于1,建立方程,解之即可;
(4)分三种情况,画出图形,分别算出即可.
解答 解:(1)将A(-3,0),B(-1,0)代入y=x2+bx+c得:$\left\{\begin{array}{l}{9-3b+c=0}\\{1-b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=4}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为:y=x2+4x+3;
(2)不等式kx+b>x2+bx+c等价于一次函数的图象高于二次函数的图象,
由图象可知在A与O之间这个范围内,一次函数的图象高于二次函数的图象,
∴-3<x<0;
(3)∵A(-3,0),B(-1,0),
∴AB=2,
如图: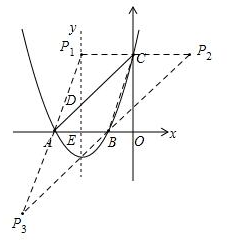
若P1ABC为平行四边形,则P1C∥AB,且P1C=AB,
则P1(-2,3);
若CABP2为平行四边形,则P2C∥AB,且P2C=AB,
则P2(2,3);
若CAP3B为平行四边形,则BC∥P3A,且BC=P3A,
则P3(-4,-3);
综上所述:满足要求的P点坐标为:(-2,3),(2,3),(-4,-3).
点评 本题考查了待定系数法求二次函数解析式、图象法解不等式、平行四边形的性质等知识点,难度适中.第(1)问体现图形结合的思想和方法,这一方法将在今后的数学学习中大量运用,要引起重视;第(3)问是常规考法,注意分类讨论,考虑周全,不要漏解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
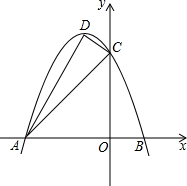 已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.
已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
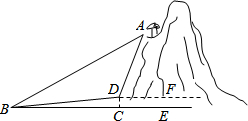 我市AAAA景区有一处景观奇异的望天洞,D点是望天洞的入口,游人从入口进洞后,可经山洞到山顶的出口亭A处观光,最后坐缆车沿索道AB返回山脚下B处.在同一平面内,若测得斜坡BD的长为120米,坡角为∠DBC=10°,在B出测得A的仰角∠ABC=40°,在D出测得A的仰角∠ADF=85°,过点D作地面BE的垂线,垂足为C.
我市AAAA景区有一处景观奇异的望天洞,D点是望天洞的入口,游人从入口进洞后,可经山洞到山顶的出口亭A处观光,最后坐缆车沿索道AB返回山脚下B处.在同一平面内,若测得斜坡BD的长为120米,坡角为∠DBC=10°,在B出测得A的仰角∠ABC=40°,在D出测得A的仰角∠ADF=85°,过点D作地面BE的垂线,垂足为C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
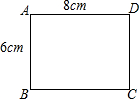 在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )
在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com