
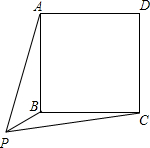
 点P是正方形ABCD外一点,PB=12cm,△APB的面积是90cm2,△CPB的面积是48cm2.请你回答:正方形ABCD的面积是多少cm2?
点P是正方形ABCD外一点,PB=12cm,△APB的面积是90cm2,△CPB的面积是48cm2.请你回答:正方形ABCD的面积是多少cm2? 分析 由于△APB与△CPB共底,因此,分别作出PB上的高就找到了解决问的突破口.具体而言,作AE垂直PB于E,作CF垂直PB于F,△APB与△CPB面积已知,PB也已知,则可求出CF和AE,易证三角形ABE与三角形BCF全等,然后用勾股定求出正方形边长的平方,即正方形面积.
解答 解:如图,作AE垂直PB于E,作CF垂直PB于F,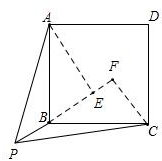
则${S}_{△PAB}=\frac{1}{2}×PB×AE$,${S}_{△PCB}=\frac{1}{2}×PB×CF$,
∵S△PAB=90,S△PCB=48,PB=12,
∴AE=15,CF=8,
∵∠ABE+∠CBF=∠ABE+∠BAE=90°,
∴∠CBF=∠BAE,
在△CBF和△BAE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠BAE=∠CBF}\\{∠AEB=∠BFC}\end{array}\right.$,
∴△CBF≌△BAE(AAS),
∴BE=CF=8,
在Rt△ABE中,AB2=AE2+BE2=225+64=289,
即正方形的面积为289.
点评 本题主要考查了正方形的性质、面积的计算、全等三角形的判定与性质,难度适中,是一道好题.作出共底的两个三角形的高线,从而构造全等三角形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
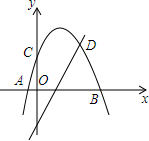 如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B,C三点,且AB=4,点D(2,$\frac{3}{2}$)在抛物线上,直线l是一次函数y=kx-2(k≠0)的图象,点O是坐标原点.
如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B,C三点,且AB=4,点D(2,$\frac{3}{2}$)在抛物线上,直线l是一次函数y=kx-2(k≠0)的图象,点O是坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com