
【题目】如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(﹣1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是_____.
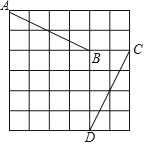
【答案】(1,1)或(4,4).
【解析】
分点A的对应点为C或D两种情况考虑:①当点A的对应点为点C时, 连接AC、 BD, 分别作线段AC、BD的垂直平分线交于点E, 点E即为旋转中心;②当点A的对应点为点D时, 连接AD、 BC, 分别作线段AD、 BC的垂直平分线交于点M, 点M即为旋转中心. 此题得解.
解:①当点A的对应点为点C时,连接AC、BD,分别作线段AC、BD 的垂直平分线交于点E,如图1所示,
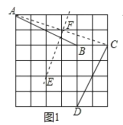
![]() A点的坐标为(-1,5),B点的坐标为(3,3),
A点的坐标为(-1,5),B点的坐标为(3,3),
![]() E点的坐标为(1,1);
E点的坐标为(1,1);
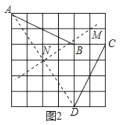
②当点A的对应点为点D时,连接AD,BC,分别作线段AD、BC的垂直平分线交于点M,
如图②所示,
![]() A点的坐标为(-1,5),B点的坐标为(3,3),
A点的坐标为(-1,5),B点的坐标为(3,3),![]() M点的坐标为(4,4).
M点的坐标为(4,4).
综上所述: 这个旋转中心的坐标为(1,1)或(4,4).
故答案为:(1,1)或(4,4).


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
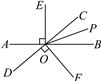
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,EO⊥AB于点O,FO⊥CD于点O.
(1)图中除直角外,还有其他相等的角,请写出两对:①______________;②______________.
(2)如果∠AOD=40°,那么:
①根据__________,可得∠BOC=________;
②求∠POF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+k(k为正整数)与坐标轴所构成的直角三角形的面积为Sk , 当k分别为1,2,3,…,199,200时,则S1+S2+S3+…+S199+S200=( )
A.10000
B.10050
C.10100
D.10150
查看答案和解析>>
科目:初中数学 来源: 题型:
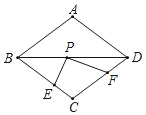
【题目】如图,在周长为12的菱形ABCD中,CE=1,CF=2,若点P为对角线BD上一动点,则PE+PF的最小值是( )
A. ![]() B. 2 C. 3 D. 5
B. 2 C. 3 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC. 
(1)求证:EF是⊙O的切线;
(2)求证:AC2=ADAB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
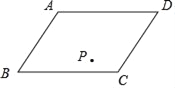
【题目】现有一块平行四边形田地ABCD要平均分给甲、乙两人,由于在这块地里有一口水井P,如图所示,为了甲,乙两人都能方便使用这口井,请你用所学的数学知识帮助甲,乙两人平均划分该田地.
要求:作图,写出划分方案,并证明你的划分方案符合要求.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘 AB、CD 是否平行;
(2)若 AB∥CD,连接 BC,过点 A 作 AM⊥BC 于 M,垂足为 M,画出图形,并写出∠BCD 与∠BAM 的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数 ![]() 的图象交EF于点B,则点B的坐标为 .
的图象交EF于点B,则点B的坐标为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com