
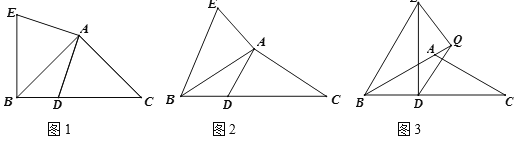
ЁОЬтФПЁПЁїABCжаЃЌЁЯBAC=ІСЁуЃЌAB=ACЃЌDЪЧBCЩЯвЛЕуЃЌНЋADШЦЕуAЫГЪБеыа§зЊІСЁуЃЌЕУЕНЯпЖЮAEЃЌСЌНгBEЃЎ
ЃЈ1ЃЉЃЈЬиР§ИажЊЃЉШчЭМ1ЃЌШєІС=90ЃЌдђBD+BEгыABЕФЪ§СПЙиЯЕЪЧ ЃЎ
ЃЈ2ЃЉЃЈРрБШЬНОПЃЉШчЭМ2ЃЌШєІС=120ЃЌЪдЬНОПBD+BEгыABЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
ЃЈ3ЃЉЃЈЭиеЙбгЩьЃЉШчЭМ3ЃЌШєІС=120ЃЌAB=AC=4ЃЌBD=![]() ЃЌQЮЊBAбгГЄЯпЩЯЕФвЛЕуЃЌНЋQDШЦЕуQЫГЪБеыа§зЊ120ЁуЃЌЕУЕНЯпЖЮQEЃЌDEЁЭBCЃЌЧѓAQЕФГЄЃЎ
ЃЌQЮЊBAбгГЄЯпЩЯЕФвЛЕуЃЌНЋQDШЦЕуQЫГЪБеыа§зЊ120ЁуЃЌЕУЕНЯпЖЮQEЃЌDEЁЭBCЃЌЧѓAQЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌМћНтЮіЃЛЃЈ3ЃЉ
ЃЌМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнSASПЩжЄЁїABEЁеЁїACDЃЌНјЖјПЩЕУBE=CDЃЌНсКЯBD+CD=BCПЩЕУBD+ BE=BCЃЌдйИљОнЕШбќжБНЧШ§НЧаЮжаBC=![]() МДПЩжЄЕУ
МДПЩжЄЕУ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§ЕуAзїAHЁЭBCЃЌИљОнЁЯBAC=120ЁуЃЌAB=ACПЩЕУЁЯABC=30ЁуЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌгЩЃЈ1ЃЉПЩжЊBD+ BE=BCЃЌгЩДЫМДПЩЕУ
ЃЌгЩЃЈ1ЃЉПЩжЊBD+ BE=BCЃЌгЩДЫМДПЩЕУ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЙ§QЕузїQFЁЮACНЛBCбгГЄЯпгкЕуFЃЌЯШжЄЁЯBQF =120ЁуЃЌBQ=QFЃЌНјЖјПЩгЩЃЈ2ЃЉЭЌРэПЩжЊЃЌЁїQBEЁеЁїQFDЃЌ![]() ЃЌНјЖјПЩжЄЕУ
ЃЌНјЖјПЩжЄЕУ![]() ЃЌдйИљОнcosЁЯEBD=
ЃЌдйИљОнcosЁЯEBD=![]() =cos60Ёу=
=cos60Ёу=![]() ПЩЧѓЕУ
ПЩЧѓЕУ![]() ЃЌНјЖјЧѓЕУ
ЃЌНјЖјЧѓЕУ![]() ЃЌзюКѓИљОнAQ=BQЃABМДПЩЕУЕНД№АИЃЎ
ЃЌзюКѓИљОнAQ=BQЃABМДПЩЕУЕНД№АИЃЎ
НтЃКЃЈ1ЃЉ![]()
РэгЩШчЯТЃК
ЁпЁЯEAD=ЁЯBAC=90Ёу
ЁрЁЯEAB=ЁЯDAC
дкЁїABEгыЁїACDжаЃЌ
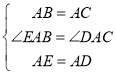
ЁрЁїABEЁеЁїACDЃЈSASЃЉ
ЁрBE=CDЃЌ
ЁпBD+CD=BC
ЁрBD+ BE=BC
ЁпдкRtЁїABCжаЃЌЁЯBAC=90ЁуЃЌAB=ACЃЌ
ЁрBC=![]()
ЁрBD+ BE=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉНсТлЃК![]() ЃЌ
ЃЌ
РэгЩШчЯТЃК
Й§ЕуAзїAHЁЭBCЃЌ
ЁпЁЯBAC=120ЁуЃЌAB=AC
ЁрЁЯABC=30ЁуЃЌ![]()
дкRtЁїABHжаЃЌcosЁЯABH=![]() =cos30Ёу=
=cos30Ёу=![]()
ЁрBH=![]() ABЃЌ
ABЃЌ
Ёр![]()
гЩЃЈ1ЃЉЭЌРэПЩжЊBD+ BE=BCЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЙ§QЕузїQFЁЮACНЛBCбгГЄЯпгкЕуFЃЌ

![]()
Ёр![]()
ЁрЁЯQFC=ЁЯQBF =30ЁуЃЌЁЯBQF =120Ёу
ЁрBQ=QF
гЩЃЈ2ЃЉЭЌРэПЩжЊЃЌЁїQBEЁеЁїQFDЃЌ![]()
![]()
![]()
![]()
ЁрcosЁЯEBD=![]() =cos60Ёу=
=cos60Ёу=![]()
![]()
Ёп![]()
![]()
![]() ЃЌ
ЃЌ
ЁрAQ=BQЃAB=![]() ЃЎ
ЃЎ


 AМгН№Ьт ЯЕСаД№АИ
AМгН№Ьт ЯЕСаД№АИ ШЋгХВтЪдОэЯЕСаД№АИ
ШЋгХВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЎАыОЖЮЊ
ЃЎАыОЖЮЊ![]() ЕФдВ
ЕФдВ![]() гыБп
гыБп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() гыБп
гыБп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() СЌНс
СЌНс![]() ВЂбгГЄЃЌгыЯпЖЮ
ВЂбгГЄЃЌгыЯпЖЮ![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБ![]() ЪБЃЌСЌНс
ЪБЃЌСЌНс![]() Шє
Шє![]() гы
гы![]() ЯрЫЦЃЌЧѓ
ЯрЫЦЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉШє![]() Чѓ
Чѓ![]() ЕФе§ЧажЕЃЛ
ЕФе§ЧажЕЃЛ
ЃЈ3ЃЉШє![]() ЃЌЩш
ЃЌЩш![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЕФКЏЪ§ЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=BCЃЌADЁЭBCгкЕуDЃЌBEЁЭACгкЕуEЃЌADгыBEНЛгкЕуFЃЌBHЁЭABгкЕуBЃЌЕуMЪЧBCЕФжаЕуЃЌСЌНгFMВЂбгГЄНЛBHгкЕуHЃЎ

ЃЈ1ЃЉШчЭМЂйЫљЪОЃЌШєЁЯABC=30ЁуЃЌЧѓжЄЃКDF+BH=![]() BDЃЛ
BDЃЛ
ЃЈ2ЃЉШчЭМЂкЫљЪОЃЌШєЁЯABC=45ЁуЃЌШчЭМЂлЫљЪОЃЌШєЁЯABC=60ЁуЃЈЕуMгыЕуDжиКЯЃЉЃЌВТЯыЯпЖЮDFЁЂBHгыBDжЎМфгжгадѕбљЕФЪ§СПЙиЯЕЃПЧыжБНгаДГіФуЕФВТЯыЃЌВЛашжЄУї.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЮЊ
ЮЊ![]() жБОЖЃЌ
жБОЖЃЌ![]() ЕуЮЊАыОЖ
ЕуЮЊАыОЖ![]() ЩЯвьгк
ЩЯвьгк![]() ЕуКЭ
ЕуКЭ![]() ЕуЕФвЛИіЕуЃЌЙ§
ЕуЕФвЛИіЕуЃЌЙ§![]() ЕузїгыжБОЖ
ЕузїгыжБОЖ![]() ДЙжБЕФЯв
ДЙжБЕФЯв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌзї
ЃЌзї![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гк
гк![]() ЕуЃЌСЌНг
ЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гк
гк![]() ЕуЃЎ
ЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЧыВТЯы![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЎ
ЕФЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН4cmЃЌBCЃН5cmЃЌЕуDдкBCЩЯЃЌЧвCDЃН3cmЃЎЖЏЕуPЃЌQЭЌЪБДгЕуCГіЗЂЃЌОљвд1cm/sЕФЫйЖШдЫЖЏЃЌЦфжаЕуPбиCAЯђжеЕуAдЫЖЏЃЛЕуQбиCBЯђжеЕуBдЫЖЏЃЎЙ§ЕуPзїPEЁЮBCЃЌЗжБ№НЛADЃЌABгкЕуEЃЌFЃЌЩшЖЏЕуQдЫЖЏЕФЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉЧѓDQЕФГЄЃЈгУКЌtЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉвдЕуQЃЌDЃЌFЃЌEЮЊЖЅЕуЮЇГЩЕФЭМаЮУцЛ§ЮЊSЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉСЌНгPQЃЌШєЕуMЮЊPQжаЕуЃЌдкећИідЫЖЏЙ§ГЬжаЃЌжБНгаДГіЕуMдЫЖЏЕФТЗОЖГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНИіЙЄГЬЖгМЦЛЎаоНЈвЛЬѕГЄ15ЧЇУзЕФЯчДхЙЋТЗЃЌвбжЊМзЙЄГЬЖгУПЬьБШввЙЄГЬЖгУПЬьЖраоТЗ0.5ЧЇУзЃЌввЙЄГЬЖгЕЅЖРЭъГЩаоТЗШЮЮёЫљашЬьЪ§ЪЧМзЙЄГЬЖгЕЅЖРЭъГЩаоТЗШЮЮёЫљашЬьЪ§ЕФ1.5БЖЃЎ
ЃЈ1ЃЉЧѓМзЁЂввСНИіЙЄГЬЖгУПЬьИїаоТЗЖрЩйЧЇУзЃП
ЃЈ2ЃЉШєМзЙЄГЬЖгУПЬьЕФаоТЗЗбгУЮЊ0.5ЭђдЊЃЌввЙЄГЬЖгУПЬьЕФаоТЗЗбгУЮЊ0.4ЭђдЊЃЌвЊЪЙСНИіЙЄГЬЖгаоТЗзмЗбгУВЛГЌЙ§5.2ЭђдЊЃЌМзЙЄГЬЖгжСЩйаоТЗЖрЩйЬьЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЊдкФГЖЋЮїзпЯђЕФAЁЂBСНЕижЎМфаовЛЬѕБЪжБЕФЙЋТЗЃЌдкЙЋТЗЦ№ЕуAДІВтЕУФГХЉЛЇCдкAЕФББЦЋЖЋ68ЁуЗНЯђЩЯЃЎдкЙЋТЗжеЕуBДІВтЕУИУХЉЛЇcдкЕуBЕФББЦЋЮї45ЁуЗНЯђЩЯЃЎвбжЊAЁЂBСНЕиЯрОр2400УзЃЎ
ЃЈ1ЃЉЧѓХЉЛЇcЕНЙЋТЗBЕФОрРыЃЛЃЈВЮПМЪ§ОнЃКsin22ЁуЁж![]() ЃЌcos22ЁуЁж
ЃЌcos22ЁуЁж![]() ЃЌtan22ЁуЁж
ЃЌtan22ЁуЁж![]() ЃЉ
ЃЉ
ЃЈ2ЃЉЯждкгЩгкШЮЮёНєМБЃЌвЊЪЙИУаоТЗЙЄГЬБШдМЦЛЎЬсЧА4ЬьЭъГЩЃЌашНЋИУЙЄГЬдЖЈЕФЙЄзїаЇТЪЬсИп20%ЃЌЧѓдМЦЛЎИУЙЄГЬЖгАЬьаоТЗЖрЩйУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЮЊСЫдіЧПбЇЩњЬхжЪЃЌЗсИЛПЮгрЩњЛюЃЌОіЖЈПЊЩшвдЯТЬхг§ПЮЭтЛюЖЏЯюФПЃКAЃЎРКЧђЃЌBЃЎЦЙХвЧђЃЌCЃЎг№УЋЧђЃЌDЃЎзуЧђЃЎЮЊСЫНтбЇЩњзюЯВЛЖФФвЛжжЛюЖЏЯюФПЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌВЂНЋЕїВщНсЙћЛцжЦГЩСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыЛиД№ЯТСаЮЪЬтЃК

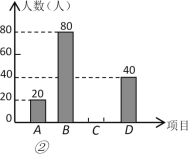
ЃЈ1ЃЉетДЮБЛЕїВщЕФбЇЩњЙВгаЁЁ ЁЁШЫЃЌдкЩШаЮЭГМЦЭМжаBЧјгђЕФдВаФНЧЖШЪ§ЮЊ ЃЛ
ЃЈ2ЃЉЧыФуНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉдкЦНЪБЕФЦЙХвЧђЯюФПбЕСЗжаЃЌМзЁЂввЁЂБћЁЂЖЁЫФШЫБэЯжгХауЃЌбЇаЃОіЖЈДгетЫФУћЭЌбЇжаШЮбЁСНУћВЮМгЪаЦЙХвЧђБШШќЃЌЧѓЧЁКУбЁжаМзЁЂввСНЮЛЭЌбЇЕФИХТЪЃЈгУЪїзДЭМЛђСаБэЗЈНтД№ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
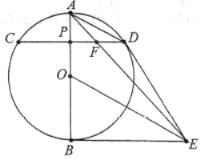
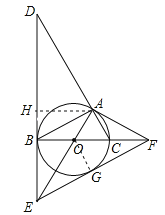
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌBCЪЧЁбOЕФжБОЖЃЌЁЯABC=30ЁуЃЌЙ§ЕуBзїЁбOЕФЧаЯпBDЃЌгыCAЕФбгГЄЯпНЛгкЕуDЃЌгыАыОЖAOЕФбгГЄЯпНЛгкЕуEЃЌЙ§ЕуAзїЁбOЕФЧаЯпAFЃЌгыжБОЖBCЕФбгГЄЯпНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїACFЁзЁїDAEЃЛ
ЃЈ2ЃЉШєSЁїAOC=![]() ЃЌЧѓDEЕФГЄЃЛ
ЃЌЧѓDEЕФГЄЃЛ
ЃЈ3ЃЉСЌНгEFЃЌЧѓжЄЃКEFЪЧЁбOЕФЧаЯпЃЎ
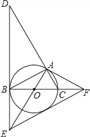
ЁОД№АИЁП(1) МћНтЮі; (2)3![]() ;(3)МћНтЮі.
;(3)МћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОндВжмНЧЖЈРэЕУЕНЁЯBAC=90ЁуЃЌИљОнШ§НЧаЮЕФФкНЧКЭЕУЕНЁЯACB=60ЁуИљОнЧаЯпЕФаджЪЕУЕНЁЯOAF=90ЁуЃЌЁЯDBC=90ЁуЃЌгкЪЧЕУЕНЁЯD=ЁЯAFC=30ЁугЩЯрЫЦШ§НЧаЮЕФХаЖЈЖЈРэМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉИљОнSЁїAOC=![]() ЃЌЕУЕНSЁїACF=
ЃЌЕУЕНSЁїACF=![]() ЃЌЭЈЙ§ЁїACFЁзЁїDAEЃЌЧѓЕУSЁїDAE=
ЃЌЭЈЙ§ЁїACFЁзЁїDAEЃЌЧѓЕУSЁїDAE=![]() ЃЌЙ§AзїAHЁЭDEгкHЃЌНтжБНЧШ§НЧаЮЕУЕНAH=
ЃЌЙ§AзїAHЁЭDEгкHЃЌНтжБНЧШ§НЧаЮЕУЕНAH=![]() DH=
DH=![]() DEЃЌгЩШ§НЧаЮЕФУцЛ§ЙЋЪНСаЗНГЬМДПЩЕУЕННсТлЃЛ
DEЃЌгЩШ§НЧаЮЕФУцЛ§ЙЋЪНСаЗНГЬМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНOE=OFЃЌИљОнЕШбќШ§НЧаЮЕФаджЪЕУЕНЁЯOFG=![]() ЃЈ180ЁуЉЁЯEOFЃЉ=30ЁуЃЌгкЪЧЕУЕНЁЯAFO=ЁЯGFOЃЌЙ§OзїOGЁЭEFгкGЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНOG=OAЃЌМДПЩЕУЕННсТлЃЎ
ЃЈ180ЁуЉЁЯEOFЃЉ=30ЁуЃЌгкЪЧЕУЕНЁЯAFO=ЁЯGFOЃЌЙ§OзїOGЁЭEFгкGЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНOG=OAЃЌМДПЩЕУЕННсТлЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉжЄУїЃКЁпBCЪЧЁбOЕФжБОЖЃЌЁрЁЯBAC=90ЁуЃЌЁпЁЯABC=30ЁуЃЌЁрЁЯACB=60Ёу
ЁпOA=OCЃЌЁрЁЯAOC=60ЁуЃЌЁпAFЪЧЁбOЕФЧаЯпЃЌЁрЁЯOAF=90ЁуЃЌЁрЁЯAFC=30ЁуЃЌЁпDEЪЧЁбOЕФЧаЯпЃЌЁрЁЯDBC=90ЁуЃЌЁрЁЯD=ЁЯAFC=30ЃЌЁпЁЯDAE=ACF=120ЁуЃЌЁрЁїACFЁзЁїDAEЃЛ
ЃЈ2ЃЉЁпЁЯACO=ЁЯAFC+ЁЯCAF=30Ёу+ЁЯCAF=60ЁуЃЌЁрЁЯCAF=30ЁуЃЌЁрЁЯCAF=ЁЯAFCЃЌЁрAC=CFЃЌЁрOC=CFЃЌЁпSЁїAOC=![]() ЃЌЁрSЁїACF=
ЃЌЁрSЁїACF=![]() ЃЌЁпЁЯABC=ЁЯAFC=30ЁуЃЌЁрAB=AFЃЌЁпAB=
ЃЌЁпЁЯABC=ЁЯAFC=30ЁуЃЌЁрAB=AFЃЌЁпAB=![]() BDЃЌЁрAF=
BDЃЌЁрAF=![]() BDЃЌЁрЁЯBAE=ЁЯBEA=30ЁуЃЌЁрAB=BE=AFЃЌЁр
BDЃЌЁрЁЯBAE=ЁЯBEA=30ЁуЃЌЁрAB=BE=AFЃЌЁр![]() ЃЌЁпЁїACFЁзЁїDAEЃЌЁр
ЃЌЁпЁїACFЁзЁїDAEЃЌЁр![]() =
=![]() ЃЌЁрSЁїDAE=
ЃЌЁрSЁїDAE=![]() ЃЌЙ§AзїAHЁЭDEгкHЃЌЁрAH=
ЃЌЙ§AзїAHЁЭDEгкHЃЌЁрAH=![]() DH=
DH=![]() DEЃЌЁрSЁїADE=
DEЃЌЁрSЁїADE=![]() DEAH=
DEAH=![]() ЁС
ЁС![]()
![]() =
=![]() ЃЌЁрDE=
ЃЌЁрDE=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпЁЯEOF=ЁЯAOB=120ЁуЃЌЁрЁЯOEB=ЁЯAFOЃЌдкЁїAOFгыЁїBOEжаЃЌЁпЁЯOBE=ЁЯOAFЃЌЁЯOEB=ЁЯAFOЃЌOA=OBЃЌЁрЁїAOFЁеЁїBEOЃЌЁрOE=OFЃЌЁрЁЯOFG=![]() ЃЈ180ЁуЉЁЯEOFЃЉ=30ЁуЃЌЁрЁЯAFO=ЁЯGFOЃЌЙ§OзїOGЁЭEFгкGЃЌЁрЁЯOAF=ЁЯOGF=90ЁуЃЌдкЁїAOFгыЁїOGFжаЃЌЁпЁЯOAF=ЁЯOGFЃЌЁЯAFO=ЁЯGFOЃЌOF=OFЃЌЁрЁїAOFЁеЁїGOFЃЌЁрOG=OAЃЌЁрEFЪЧЁбOЕФЧаЯпЃЎ
ЃЈ180ЁуЉЁЯEOFЃЉ=30ЁуЃЌЁрЁЯAFO=ЁЯGFOЃЌЙ§OзїOGЁЭEFгкGЃЌЁрЁЯOAF=ЁЯOGF=90ЁуЃЌдкЁїAOFгыЁїOGFжаЃЌЁпЁЯOAF=ЁЯOGFЃЌЁЯAFO=ЁЯGFOЃЌOF=OFЃЌЁрЁїAOFЁеЁїGOFЃЌЁрOG=OAЃЌЁрEFЪЧЁбOЕФЧаЯпЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
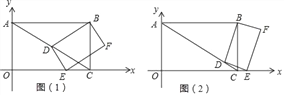
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊдЕуЃЌЫФБпаЮABCOЪЧОиаЮЃЌЕуAЃЌCЕФзјБъЗжБ№ЪЧAЃЈ0ЃЌ2ЃЉКЭCЃЈ2![]() ЃЌ0ЃЉЃЌЕуDЪЧЖдНЧЯпACЩЯвЛЖЏЕуЃЈВЛгыAЃЌCжиКЯЃЉЃЌСЌНсBDЃЌзїDEЁЭDBЃЌНЛxжсгкЕуEЃЌвдЯпЖЮDEЃЌDBЮЊСкБпзїОиаЮBDEFЃЎ
ЃЌ0ЃЉЃЌЕуDЪЧЖдНЧЯпACЩЯвЛЖЏЕуЃЈВЛгыAЃЌCжиКЯЃЉЃЌСЌНсBDЃЌзїDEЁЭDBЃЌНЛxжсгкЕуEЃЌвдЯпЖЮDEЃЌDBЮЊСкБпзїОиаЮBDEFЃЎ
ЃЈ1ЃЉЬюПеЃКЕуBЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЪЧЗёДцдкетбљЕФЕуDЃЌЪЙЕУЁїDECЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіADЕФГЄЖШЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЂйЧѓжЄЃК![]() ЃЛ
ЃЛ
ЂкЩшAD=xЃЌОиаЮBDEFЕФУцЛ§ЮЊyЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЈПЩРћгУЂйЕФНсТлЃЉЃЌВЂЧѓГіyЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com