
����Ŀ���Ķ�������ϣ����(1)-(3)�⣮
��ѧ���ϣ���ʦ��ʾ������һ���⣺
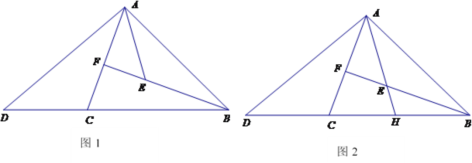
��ͼ1���ڡ�ABC�У�BA=BC��![]() ����F��AC�ϣ���E��BF�ϣ�
����F��AC�ϣ���E��BF�ϣ�![]() ����D��BC �ӳ����ϣ�����AD��AE����ACD+��DAE=180�b��̽���߶�AD��AE��������ϵ��֤����
����D��BC �ӳ����ϣ�����AD��AE����ACD+��DAE=180�b��̽���߶�AD��AE��������ϵ��֤����
ͬѧ�Ǿ���˼�����������ѵ��뷨��
С������ͨ���۲�Ͷ��������֡�CAD���EAB��ȣ���
С������ͨ���۲�Ͷ��������֡�FAE���DҲ��ȣ���
Сΰ����ͨ���߽ǹ�ϵ���츨���ߣ�������һ�����������Եõ��߶�AD��AE��������ϵ����
![]()
��ʦ��������ԭ���������ӳ�ͼ1�е�AE����BC�ཻ�ڵ�H(��ͼ2)����֪��DH��AH��������ϵ���������![]() ��ֵ����
��ֵ����
��1����֤����CAD=��EAB��
��2����![]() ��ֵ���ú�k��ʽ�ӱ�ʾ����
��ֵ���ú�k��ʽ�ӱ�ʾ����
��3����ͼ2����![]() ����
����![]() ��ֵΪ________���ú�k��ʽ�ӱ�ʾ����
��ֵΪ________���ú�k��ʽ�ӱ�ʾ����
���𰸡���1������������2��![]() ����3��
����3��![]() ��
��
��������
��1������BA=BC�ó���BAC=��BCA���ٸ�����������Ǻ͵�֪ʶ���ACD+��DAE=180�b����ACD+��ACB=180�b�ó���DAC=��BAE��
��2������һ������C����ACM=��ABE����AD�ڵ�M��֤������AEB�ס�AMC���������Ʊȵó�![]() ��
��![]() ���ٸ���������֤��DCM�ס�AFE���������Ʊȵõ�
���ٸ���������֤��DCM�ס�AFE���������Ʊȵõ�![]() ��AD=AM+DM=
��AD=AM+DM=![]() ���������
���������
������������B��BN��AC��AE�ӳ����ڵ�N��֤����AFE�ס�NBE����ACD�ס�ABN���������Ʊ���⼴�ɣ�
��3������B��BN��AC��AE�ӳ����ڵ�N����֤��AHC��DHA���������Ʊȵõ�![]() ������
������![]() ��
��![]() ���ó�
���ó�![]() ����AH=2a��AB=BC=b��
����AH=2a��AB=BC=b��
����EH=AH-AE=EN-NH�����Ƶó�![]() ��
��![]() �����ɡ�ADH�ס�NBH��������������ó�
�����ɡ�ADH�ס�NBH��������������ó�![]() �����b���ɣ�
�����b���ɣ�
(1)��BA=BC��
���BAC=��BCA��
�ߡ�ACD+��DAE=180�b��
��ACD+��ACB=180�b��
���DAE=��ACB��
���DAE=��BAC��
���DAC=��BAE��
(2)����һ��
����C����ACM=��ABE����AD�ڵ�M��
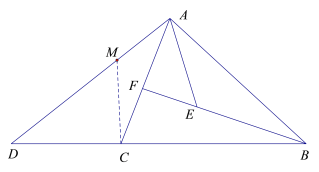
�ߡ�DAC=��BAE��
���AEB�ס�AMC��
��![]() ��
��
��![]() ��
��
��![]() ��
��
![]() ��
��
��![]() ��
��
��![]() ��
��
�ߡ�AEF=��EAB+��ABE��
��DMC=��MAC+��ACM��
���DMC=��AEF��
�ߡ�ACB=��D+��DAC��
��DAE=DAC+��FAE��
��DAE=��ACB��
���D=��FAE��
���DCM�ס�AFE��
��![]() ��
��
��![]() ��
��
��AD=AM+DM=![]() ��
��
��![]() ��
��
��������
����B��BN��AC��AE�ӳ����ڵ�N��
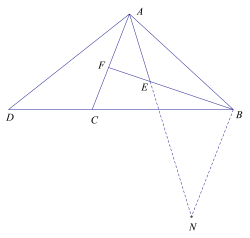
���N=��FAE��
��AFE=��EBN��
���AFE�ס�NBE��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�ߡ�ACB=��D+��DAC��
��DAE=DAC+��FAE��
��DAE=��ACB��
���D=��FAE��
�ߡ�DAC=��BAE��
���ACD�ס�ABN��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��3��ͬ������������
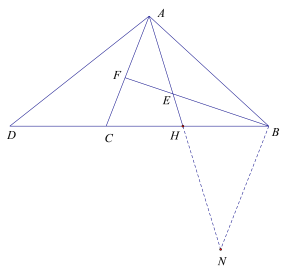
�ߡ�D=��CAH����AHC=��DHA��
���AHC��DHA��
��![]() ��
��
![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��AH=2a��AB=BC=b��
��DH=3a, ![]() ��
��
��NE=2AE��
��NE=b��
��EH=AH-AE=EN-NH��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���ɷ��������Ƶã�
![]() ��
��
�ߡ�ADH�ס�NBH��
��![]() ��
��
��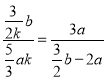 ��
��
��![]() ��
��
��![]() ���ᣩ��
���ᣩ�� ![]() ��
��
��![]() ��
��


 ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�BC�Ĵ�ֱƽ����MN��AB�ڵ�D��CDƽ�֡�ACB����AD��2��BD��3����AC�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ����Ʒ������50������Ʒ����۴�������ۣ��Ȱ�ԭ���������Щ��Ʒ�ٻ���200Ԫ��
![]() �����Ʒ�ı��Ϊ����Ԫ��
�����Ʒ�ı��Ϊ����Ԫ��
![]() ��֪����Ʒ�Ľ���Ϊÿ��12Ԫ�������г����ˣ�����
��֪����Ʒ�Ľ���Ϊÿ��12Ԫ�������г����ˣ�����![]() �б�����ۣ����̳�ÿ������100����ÿ��1Ԫ��ÿ��Ҫ����5��
�б�����ۣ����̳�ÿ������100����ÿ��1Ԫ��ÿ��Ҫ����5��![]() ��ô�Ǽۺ�Ҫʹ����Ʒÿ��������������Ӧ�����ۼ۸�Ϊÿ������Ԫ����������Ƕ��٣�
��ô�Ǽۺ�Ҫʹ����Ʒÿ��������������Ӧ�����ۼ۸�Ϊÿ������Ԫ����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0����ͼ����ͼ��ʾ���������½��ۣ���b2��4ac����2a+b��0����3a+c��0����4a��2b+c��0����9a+3b+c��0�����н�����ȷ�ĸ����У�������
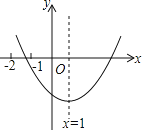
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ѧϰ�ĵã�
��ͮͬѧ��ѧϰ�ꡰԲ����һ�����ݺо���һЩ��������������Ӹ���Բ������Բ��֪ʶ���������ʹ�����÷dz����ף�
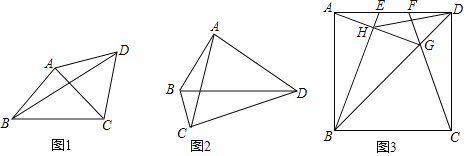
���磺��ͼ1���ڡ�ABC�У�AB��AC����BAC��90�㣬D�ǡ�ABC��һ�㣬��AD��AC�����BDC�Ķ��������Ե�AΪԲ�ģ�ABΪ�뾶��������A�����C��D������A�ϣ���BAC����A��Բ�Ľǣ�����BDC��Բ�ܽǣ��Ӷ������õ���BDC���� ���㣮
��2������������
��ͼ2�����ı���ABCD�У���BAD����BCD��90�㣬��BDC��25�㣬���BAC�Ķ�����
��3����������չ��
��ͼ3����ͼ��E��F��������ABCD�ı�AD���������㣬����AE��DF������CF��BD�ڵ�G������BE��AG�ڵ�H���������εı߳�Ϊ2�����߶�DH���ȵ���Сֵ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������ݳ�����ͨѹ���������ϲ�����ͨ������4.18�������裮ij���̶ӳе���ij��·900�׳��ĸ��������̶��ڸ�����360��·�����������豸��ÿ��Ĺ���Ч�ʱ�ԭ�������20%���������27��������������������豸ǰ���̶�ÿ������·�����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������������ȫ���������д����������ijУ�ڽ�ѧ¥�����½���һ����������ƣ�����ͼ��С��ͬѧΪ���������Ƶĸ߶�![]() ����վ�ھ����ѧ¥�ײ�
����վ�ھ����ѧ¥�ײ�![]() ��6��Զ�ĵ���
��6��Զ�ĵ���![]() ������������Ƶĵײ�
������������Ƶĵײ�![]() ������Ϊ
������Ϊ![]() ��ͬʱ��ý�ѧ¥����
��ͬʱ��ý�ѧ¥����![]() ��������Ϊ
��������Ϊ![]() (
(![]() ��
��![]() ��
��![]() ��
��![]() ��ͬһֱ����)��Ȼ��С�����¶�
��ͬһֱ����)��Ȼ��С�����¶�![]() ��б�´�
��б�´�![]() �ߵ�
�ߵ�![]() ������ʱ
������ʱ![]() ���������
���������![]() ƽ�У�
ƽ�У�
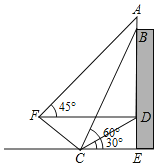
(1)���![]() ��ֱ��
��ֱ��![]() �ľ���(�����������)��
�ľ���(�����������)��
(2)��С����![]() ���ֲ�������ƶ���
���ֲ�������ƶ���![]() ������Ϊ
������Ϊ![]() ���������Ƶĸ߶�
���������Ƶĸ߶�![]() (�����ȷ��0.1�ף�
(�����ȷ��0.1�ף�![]() ��
��![]() )��
)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
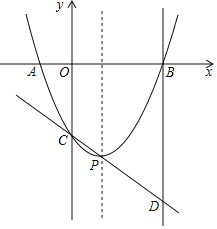
����Ŀ����ͼ�����κ���![]() ��ͼ����
��ͼ����![]() ��ĸ������������ֱ���A��B���㣬��y�ύ�ڵ�C������ΪP��ֱ��
��ĸ������������ֱ���A��B���㣬��y�ύ�ڵ�C������ΪP��ֱ��![]() �����B�Ҵ�ֱ��
�����B�Ҵ�ֱ��![]() ���ֱ�߽��ڵ�D����CP��PD=1��2��tan��PDB=
���ֱ�߽��ڵ�D����CP��PD=1��2��tan��PDB=![]() ��
��
��1����ֱ��д��A��B��������꣺A �� B ��
��2����������κ����Ľ���ʽ��
��3���������ߵĶԳ�������һ��Mʹ|MC-MB|��ֵ������M������Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C�Ľ���ʽΪy��x2+2x��3��C��x�ύ�ڵ�A��B����A�ڵ�B��ࣩ����y�ύ�ڵ�D������ΪP��
�������A��B��D��P�����ꣻ
��������������C����ֱ��PD�ķ���ƽ�Ƶõ�������C�䣻
����������C����ֱ��y��2x��5ֻ��һ��������ʱ����������C��Ľ���ʽ��
����M��xm��ym��������������C����һ�㣬����6��xm��2��ymΪ�����������������ĵ�M�ĸ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com