
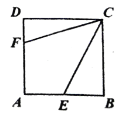
【题目】如图,正方形![]() 的边长为12,点
的边长为12,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,若
上,若![]() ,且
,且![]() ,则
,则![]() ______.
______.
【答案】![]()
【解析】
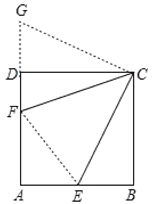
首先延长FD到G,使DG=BE,利用正方形的性质得∠B=∠CDF=∠CDG=90°,CB=CD;利用SAS定理得△BCE≌△DCG,利用全等三角形的性质易证△GCF≌△ECF,利用勾股定理可得DF,求出AF,设BE=x,利用GF=EF,解得x,再利用勾股定理可得CE.
解:如图,延长FD到G,使DG=BE;
连接CG、EF;
∵四边形ABCD为正方形,
在△BCE与△DCG中,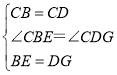 ,
,
∴△BCE≌△DCG(SAS),
∴CG=CE,∠DCG=∠BCE,
∴∠GCF=45°,
在△GCF与△ECF中,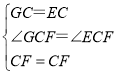 ,
,
∴△GCF≌△ECF(SAS),
∴GF=EF,
∵DF=![]() ,AB=AD=12,
,AB=AD=12,
∴AF=124=8,
设BE=x,则AE=12x,EF=GF=4+x,
在Rt△AEF中,由勾股定理得:(12x)2+82=(4+x)2,
解得:x=6,
∴BE=6,
∴CE=![]() ,
,
故答案为:![]() .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
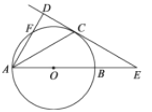
(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,![]() ≈1.73,结果保留一位小数.)
≈1.73,结果保留一位小数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣6,点B在数轴上A点右侧,且AB=14,动点M从点A出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点M表示的数 (用含t的式子表示);
(2)动点N从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点M,N同时出发,问点M运动多少秒时追上点N?
(3)若P为AM的中点,F为MB的中点,点M在运动过程中,线段PF的长度是否发生变化?若变化,请说明理由;若不变,请求出线段PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)(﹣3)×(+4)﹣48÷|﹣6|
(2)77°53'26″+33.3°(结果用度分秒形式表示)
(3)[﹣14﹣(1﹣0.5×![]() )]×[3﹣(﹣3)2]
)]×[3﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
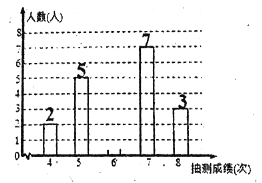
【题目】为了解某校八年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成两个不完整的统计图,请结合图中信息回答下列问题:
(1)本次抽测的男生有 人,请将条形图补充完成,本次抽测成绩的中位数是 次;
(2)若规定引体向上6次及其以上为体能达标,则该校500名八年级男生中估计有多少人体能达标?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,b,我们可以用min{a,b}表示a,b两数中较小的数,例如min{3,-1}=-1,min{2,2}=2. 类似地,若函数y1、y2都是x的函数,则y=min{y1, y2}表示函数y1和y2的“取小函数”.
(1)设y1=x,y2=![]() ,则函数y=min{x,
,则函数y=min{x, ![]() }的图像应该是 中的实线部分.
}的图像应该是 中的实线部分.

(2)请在下图中用粗实线描出函数y=min{(x-2)2, (x+2)2}的图像,并写出该图像的三条不同性质:

① ;
② ;
③ ;
(3)函数y=min{(x-4)2, (x+2)2}的图像关于 对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张华随爸爸来西安游玩,他们还有四个旅游景点没去,分别是西安以东的兵马俑和华山,西安以西的乾陵和法门寺。由于仅剩两天的时间,张华不能游玩所有风景区,于是爸爸让张华从四张旅游景点图片(大小、形状及背面图案完全相同)中抽签确定.爸爸将这四张图片背面朝上洗匀后,让张华先随机抽取一张(不放回),再抽取一张,若抽到的两个景点都在西安以东或都在西安以西,则爸爸带他到这两个景点旅游,否则只能去一个景点旅游(兵马俑、华山、乾陵、法门寺这四张图片分别用B,H,Q,F表示).
(1)求张华抽到景点兵马俑的图片的概率;
(2)请你用列表或画树状图的方法求张华能去两个景点旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
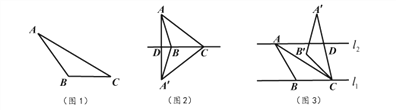
【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”。
(1)概念理解:
如图1,在![]() 中,
中,![]() ,
,![]() .
.![]() ,试判断
,试判断![]() 是否是“等高底”三角形,请说明理由.
是否是“等高底”三角形,请说明理由.
(2)问题探究:
如图2, ![]() 是“等高底”三角形,
是“等高底”三角形,![]() 是“等底”,作
是“等底”,作![]() 关于
关于![]() 所在直线的对称图形得到
所在直线的对称图形得到![]() ,连结
,连结![]() 交直线
交直线![]() 于点
于点![]() .若点
.若点![]() 是
是![]() 的重心,求
的重心,求![]() 的值.
的值.
(3)应用拓展:
如图3,已知![]() ,
,![]() 与
与![]() 之间的距离为2.“等高底”
之间的距离为2.“等高底”![]() 的“等底”
的“等底” ![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上
上![]() 的
的![]() 倍.将
倍.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,
,![]() 所在直线交
所在直线交![]() 于点
于点![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com