
����Ŀ�����Ƕ���:���һ��������һ�����ϵĸߵ���������,��ô��������ν������ȸߵ���������,�����߽�����������ε����ȵ�����
��1����������:
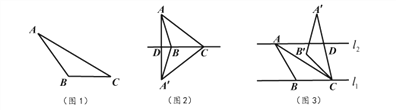
��ͼ1,��![]() ��,
��,![]() ,
,![]() .
.![]() ,���ж�
,���ж�![]() �Ƿ������ȸߵ��������Σ���˵������.
�Ƿ������ȸߵ��������Σ���˵������.
��2������̽��:
��ͼ2, ![]() �����ȸߵ���������,
�����ȸߵ���������,![]() �����ȵ�������
�����ȵ�������![]() ����
����![]() ����ֱ�ߵĶԳ�ͼ�εõ�
����ֱ�ߵĶԳ�ͼ�εõ�![]() ,����
,����![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() .����
.����![]() ��
��![]() ������,��
������,��![]() ��ֵ.
��ֵ.
��3��Ӧ����չ:
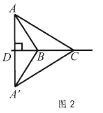
��ͼ3,��֪![]() ,
,![]() ��
��![]() ֮��ľ���Ϊ2.���ȸߵ���
֮��ľ���Ϊ2.���ȸߵ���![]() �����ȵ���
�����ȵ��� ![]() ��ֱ��
��ֱ��![]() ��,��
��,��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ��.��
��.��![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת
��˳ʱ�뷽����ת![]() �õ�
�õ�![]() ,
,![]() ����ֱ�߽�
����ֱ�߽�![]() �ڵ�
�ڵ�![]() .��
.��![]() ��ֵ.
��ֵ.
���𰸡���1��֤������������2��![]() ��3��
��3��![]() ��ֵΪ
��ֵΪ![]() ,
,![]() ,2
,2
����������1������A��AD��ֱ��CB�ڵ�D�����Եõ�AD=BC=3�����ɵõ����ۣ�
��2������ ��ABC�ǡ��ȸߵס������Σ�BC�ǡ��ȵס����õ�AD=BC�� ���� ��A��BC�릤ABC����ֱ��BC�Գƣ� �õ� ��ADC=90�㣬�����ĵ����ʣ��õ�BC=2BD����BD=x����AD=BC=2x�� CD=3x ���ɹ��ɶ�����AC=![]() x�����ɵõ����ۣ�
x�����ɵõ����ۣ�
��3��������������ۼ������ٵ�AB=![]() BCʱ���ٷ�����������ۣ�
BCʱ���ٷ�����������ۣ�
�ڵ�AC=![]() BCʱ���ٷ�����������ۼ��ɣ�
BCʱ���ٷ�����������ۼ��ɣ�
��1���ǣ��������£�
��ͼ1������A��AD��ֱ��CB�ڵ�D��
�তADCΪֱ�������Σ���ADC=90�㣮
�� ��ACB=30�㣬AC=6���� AD=![]() AC=3��
AC=3��
�� AD=BC=3��
����ABC�ǡ��ȸߵס������Σ�
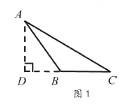
��2����ͼ2�� �� ��ABC�ǡ��ȸߵס������Σ�BC�ǡ��ȵס�����AD=BC��
�� ��A��BC�릤ABC����ֱ��BC�Գƣ� �� ��ADC=90�㣮
�ߵ�B�Ǧ�AA��C�����ģ� �� BC=2BD��
��BD=x����AD=BC=2x����CD=3x ��
���ɹ��ɶ�����AC=![]() x��
x��
��![]() ��
��
��3���ٵ�AB=![]() BCʱ��
BCʱ��
������ͼ3����AE��l1�ڵ�E�� DF��AC�ڵ�F��
�����ȸߵ��� ��ABC�����ȵ���ΪBC��l1//l2��
l1��l2֮��ľ���Ϊ2�� AB=![]() BC��
BC��
��BC=AE=2��AB=2![]() ��
��
��BE=2����EC=4����AC= ![]() ��
��
�� ��ABC�Ƶ�C��˳ʱ�뷽����ת45���õ���A' B' C�����CDF=45�㣮
��DF=CF=x ��
��l1//l2�����ACE=��DAF����![]() ����AF=2x��
����AF=2x��
��AC=3x=![]() ���ɵ�x=
���ɵ�x=![]() ����CD=
����CD=![]() x=
x=![]() ��
��
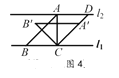
������ͼ4����ʱ��ABC�ǵ���ֱ�������Σ�
�� ��ABC�Ƶ�C��˳ʱ�뷽����ת45���õ���A' B' C��
�� ��ACD�ǵ���ֱ�������Σ�
�� CD=![]() AC=
AC=![]() ��
��
�ڵ�AC=![]() BCʱ��
BCʱ��
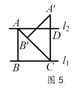
������ͼ5����ʱ��ABC�ǵ���ֱ�������Σ�
�� ��ABC�Ƶ�C��˳ʱ�뷽����ת45��õ���A�� B��C��
��A��C��l1����CD=AB=BC=2��
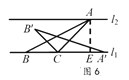
������ͼ6����AE��l1�ڵ�E����AE=BC��
��AC=![]() BC=
BC=![]() AE�����ACE=45�㣬
AE�����ACE=45�㣬
�তABC�Ƶ�C��˳ʱ�뷽����ת45��õ���A�� B��Cʱ��
��A����ֱ��l1�ϣ�
��A��C��l2����ֱ��A�� C��l2���㣮
����������CD��ֵΪ![]() ��
��![]() ��2��
��2��


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
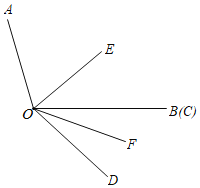
����Ŀ����֪��AOB��110������COD��40����OEƽ�֡�AOC��OFƽ�֡�BOD��
��1����ͼ�����EOF�Ķ�����
��2����ͼ����OB��OC�غ�ʱ�����AOE����BOF��ֵ��
��3������COD��ͼ��λ���Ƶ�O��ÿ��3�����ٶ�˳ʱ����תt�루0��t��10��������ת�����С�AOE����BOF��ֵ�Ƿ����t�ı仯���仯�����������仯��������ö�ֵ���������仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����籭��С����������ĸ���ӽ��е�ѭ��������ÿ������һ������ʤһ����3�֣�ƽһ����1�֣���һ����0��.ijС����������ס��ҡ��������Ķӷֱ��õ�һ�������������������ӵ��ܵ÷�ǡ�����ĸ����������������Ҵ�ƽ������ǣ� ��
A. �� B. ���붡 C. �� D. ���붡
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���¥��֮��ĵ������⣬ij�����涨������¥����ľ�������Ϊ40�ף�����12ʱ���ܵ��⣮��ͼ��ij��¥��һ¥��̨��1�ף�Ҫ�ڴ�¥���Ϸ�40�״��ٽ�һ����¥����֪�õ�����������12ʱ��������Ϸ����䣬���ҹ�����ˮƽ�ߵļн���СΪ30�����ڲ�Υ���涨������£������½�¥����߶����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������ҳ�������ͬ�ļ۸����ͬ������Ʒ��Ϊ�������˿ͣ������Ƴ���ͬ���Żݷ������ڼ׳����ۼƹ�����Ʒ����300Ԫ֮�������ְ�ԭ��8���Żݣ����ҳ����ۼƹ�����Ʒ����200Ԫ֮�������ְ�ԭ��8.5���Żݣ���˿�Ԥ���ۼƹ���![]() Ԫ(
Ԫ(![]() )��
)��
(1)���ú�![]() �Ĵ���ʽ�ֱ��ʾ�˿������ҳ��й��������ķ��ã�
�Ĵ���ʽ�ֱ��ʾ�˿������ҳ��й��������ķ��ã�
(2)����������500Ԫ����Ʒ������Ϊ��Ӧ��ȥ�ļҳ��У���˵�����ɣ�
(3)����һ�£������������Ԫ����Ʒʱ�������ҳ��й��������ķ���һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���в���ʽ���Ӧ���⣺��У��У��![]() ����������Ů����������סУ����֪��У��У�������ɼ����ᣬÿ��ס
����������Ů����������סУ����֪��У��У�������ɼ����ᣬÿ��ס![]() �ˣ�ʣ
�ˣ�ʣ![]() ����ס��ÿ��ס
����ס��ÿ��ס![]() �ˣ���һ������ס�������ʿ����ж��ټ����ᣬ������Ů����
�ˣ���һ������ס�������ʿ����ж��ټ����ᣬ������Ů����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ���ı���ABCD���ܳ���32 cm��![]() ��
��![]() ��
��![]() ��E��F�Ǵ��㣬��
��E��F�Ǵ��㣬��![]()
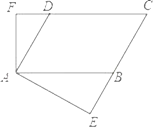
��1����![]() �Ķ�����
�Ķ�����
��2����BE��DF�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com