
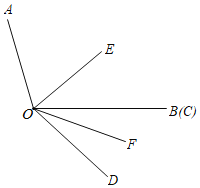
،¾جâؤ؟،؟زرضھ،دAOB£½110،م£¬،دCOD£½40،م£¬OEئ½·ض،دAOC£¬OFئ½·ض،دBOD£®
£¨1£©بçح¼£¬اَ،دEOFµؤ¶بت£®
£¨2£©بçح¼£¬µ±OB،¢OCضط؛دت±£¬اَ،دAOE©پ،دBOFµؤضµ£»
£¨3£©µ±،دCOD´سح¼µؤخ»ضأبئµمOزشأ؟أë3،مµؤثظ¶بث³ت±صëذ×ھtأ루0£¼t£¼10£©£»شعذ×ھ¹³جضذ،دAOE©پ،دBOFµؤضµتا·ٌ»لزٍtµؤ±ن»¯¶ّ±ن»¯£¬بô²»·¢ةْ±ن»¯£¬اëاَ³ِ¸أ¶¨ضµ£»بô·¢ةْ±ن»¯£¬اëثµأ÷ہيسة£®
،¾´ً°¸،؟£¨1£©،دEOF£½75،م£»£¨2£©،دAOE©پ،دBOF£½35،م£»£¨3£©،دAOE©پ،دBOF=35،م.
،¾½âخِ،؟
£¨1£©ض±½سہûسأ½ائ½·ضدكµؤذشضتاَ³ِ،دEOC؛ح،دCOF£¬دà¼س¼´؟ةاَ³ِ´ً°¸£»
£¨2£©ہûسأ½ائ½·ضدكµؤذشضتاَ³ِ،دAOE؛ح،دCOF£¬دà¼ُ¼´؟ةاَ³ِ´ً°¸£»
£¨3£©µ±OC±كبئOث³ت±صëذ×ھت±£¬،دAOBتا±ن»¯µؤ£¬،دAOB=110،م+3،مt£¬،دBODتا²»±ن»¯µؤ£¬ثùزش،دAOE-،دBOFضµتا²»±ن»¯µؤ£»
£¨1£©،كOEئ½·ض،دAOC£¬OFئ½·ض،دBOD£¬
،à،دEOF£½،دEOB+،دBOF£½![]() ،دAOB+
،دAOB+![]() ،دBOD£¬
،دBOD£¬
،ك،دAOB£½110،م£¬،دCOD£½40،م£¬
،à،دEOF£½75،م£»
£¨2£©،كOEئ½·ض،دAOC£¬OFئ½·ض،دBOD£¬،دAOB£½110،م£¬،دCOD£½40،م£¬
،à،دAOE£½55،م£¬،دBOF£½20،م£¬
،à،دAOE©پ،دBOF£½35،م£»
£¨3£©،كOFئ½·ض،دBOD£¬
،à،دBOF£½![]() ،دBOD£¬
،دBOD£¬
،ك،دAOB£½110،م£¬BO±كبئµمOزشأ؟أë3،مµؤثظ¶بث³ت±صëذ×ھtأ룬
،à،دAOB£½110،م+3،مt£¬،دBOF£½![]() £¨40،م+3،مt£©£¬
£¨40،م+3،مt£©£¬
،àOEئ½·ض،دAOB£¬
،à،دAOE£½![]() £¨110،م+3،مt£©£¬
£¨110،م+3،مt£©£¬
،à،دAOE©پ،دBOF£½![]() £¨110،م+3،مt£©©پ20،م©پ
£¨110،م+3،مt£©©پ20،م©پ![]() t£½35،م£¬
t£½35،م£¬
،àشعذ×ھ¹³جضذ،دAOE©پ،دBOFµؤضµتا²»»لزٍtµؤ±ن»¯¶ّ±ن»¯£¬،دAOE©پ،دBOF£½35،م£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬زرضھتضلةدµمA±يت¾µؤتخھ©پ6£¬µمBشعتضلةدAµمسز²à£¬ازAB£½14£¬¶¯µمM´سµمA³ِ·¢£¬زشأ؟أë5¸ِµ¥خ»³¤¶بµؤثظ¶برطتضلدٍسزشبثظشث¶¯£¬ةèشث¶¯ت±¼نخھt£¨t£¾0£©أ룮
![]()
£¨1£©ذ´³ِتضلةدµمB±يت¾µؤت،، ،،£¬µمM±يت¾µؤت،، ،،£¨سأ؛¬tµؤت½×س±يت¾£©£»
£¨2£©¶¯µمN´سµمB³ِ·¢£¬زشأ؟أë3¸ِµ¥خ»³¤¶بµؤثظ¶برطتضلدٍسزشبثظشث¶¯£¬بôµمM£¬Nح¬ت±³ِ·¢£¬ختµمMشث¶¯¶àةظأëت±×·ةدµمN£؟
£¨3£©بôPخھAMµؤضذµم£¬FخھMBµؤضذµم£¬µمMشعشث¶¯¹³جضذ£¬دك¶خPFµؤ³¤¶بتا·ٌ·¢ةْ±ن»¯£؟بô±ن»¯£¬اëثµأ÷ہيسة£»بô²»±ن£¬اëاَ³ِدك¶خPFµؤ³¤£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟¶شسعتµتa£¬b£¬خزأا؟ةزشسأmin{a£¬b}±يت¾a£¬bء½تضذ½دذ،µؤت£¬ہبçmin{3£¬£1}£½£1£¬min{2£¬2}£½2. ہàثئµط£¬بô؛¯تy1،¢y2¶¼تاxµؤ؛¯ت£¬شٍy£½min{y1£¬ y2}±يت¾؛¯تy1؛حy2µؤ،°ب،ذ،؛¯ت،±£®
£¨1£©ةèy1£½x£¬y2£½![]() £¬شٍ؛¯تy£½min{x£¬
£¬شٍ؛¯تy£½min{x£¬ ![]() }µؤح¼دٌس¦¸أتا ضذµؤتµدك²؟·ض£®
}µؤح¼دٌس¦¸أتا ضذµؤتµدك²؟·ض£®

£¨2£©اëشعدآح¼ضذسأ´ضتµدكأè³ِ؛¯تy£½min{(x£2)2£¬ (x£«2)2}µؤح¼دٌ£¬²¢ذ´³ِ¸أح¼دٌµؤبجُ²»ح¬ذشضت£؛

¢ظ £»
¢ع £»
¢غ £»
£¨3£©؛¯تy£½min{(x£4)2£¬ (x£«2)2}µؤح¼دٌ¹طسع ¶ش³ئ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟صإ»ھثو°ض°ضہ´خ÷°²سخحو£¬ثûأا»¹سذثؤ¸ِآأسخ¾°µمأ»ب¥£¬·ض±ًتاخ÷°²زش¶«µؤ±ّآيظ¸؛ح»ھة½£¬خ÷°²زشخ÷µؤا¬ءê؛ح·¨أإثآ،£سةسع½ِت£ء½جىµؤت±¼ن£¬صإ»ھ²»ؤـسخحوثùسذ·ç¾°اّ£¬سعتا°ض°ضبأصإ»ھ´سثؤصإآأسخ¾°µمح¼ئ¬£¨´َذ،،¢ذخ×´¼°±³أوح¼°¸حêب«دàح¬£©ضذ³éا©ب·¶¨.°ض°ض½«صâثؤصإح¼ئ¬±³أو³¯ةدد´شب؛َ£¬بأصإ»ھدبثو»ْ³éب،ز»صإ£¨²»·إ»ط£©£¬شظ³éب،ز»صإ£¬بô³éµ½µؤء½¸ِ¾°µم¶¼شعخ÷°²زش¶«»ٍ¶¼شعخ÷°²زشخ÷£¬شٍ°ض°ض´ّثûµ½صâء½¸ِ¾°µمآأسخ£¬·ٌشٍض»ؤـب¥ز»¸ِ¾°µمآأسخ£¨±ّآيظ¸،¢»ھة½،¢ا¬ءê،¢·¨أإثآصâثؤصإح¼ئ¬·ض±ًسأB£¬H£¬Q£¬F±يت¾£©.
£¨1£©اَصإ»ھ³éµ½¾°µم±ّآيظ¸µؤح¼ئ¬µؤ¸إآت£»
£¨2£©اëؤمسأءذ±ي»ٍ»ت÷×´ح¼µؤ·½·¨اَصإ»ھؤـب¥ء½¸ِ¾°µمآأسخµؤ¸إآت.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
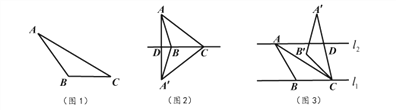
،¾جâؤ؟،؟بçح¼£¬شع،÷ABCضذ£¬،دABCخھبٌ½ا£¬µمDخھض±دكBCةدز»¶¯µم£¬زشADخھض±½ا±كازشعADµؤسز²à×÷µبرüض±½اب½اذخADE£¬،دDAE£½90،م£¬AD£½AE£®
£¨1£©بç¹ûAB£½AC£¬،دBAC£½90،م£®¢ظµ±µمDشعدك¶خBCةدت±£¬بçح¼1£¬دك¶خCE،¢BDµؤخ»ضأ¹طدµخھ___________£¬تء؟¹طدµخھ___________
¢عµ±µمDشعدك¶خBCµؤرس³¤دكةدت±£¬بçح¼2£¬¢ظضذµؤ½لآغتا·ٌبشب»³ةء¢£¬اëثµأ÷ہيسة£®
£¨2£©بçح¼3£¬بç¹ûAB،ظAC£¬،دBAC،ظ90،م£¬µمDشعدك¶خBCةدشث¶¯،£ج½¾؟£؛µ±،دACB¶àةظ¶بت±£¬CE،حBC£؟اëثµأ÷ہيسة£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ت³ئ·³§´سةْ²ْµؤ´ü×°ت³ئ·ضذ³é³ِرùئ·20´ü£¬¼ى²âأ؟´üµؤضتء؟تا·ٌ·û؛د±ê×¼£¬³¬¹»ٍ²»×مµؤ²؟·ض·ض±ًسأص،¢¸؛تہ´±يت¾£¬¼اآ¼بçدآ±ي£؛
سë±ê×¼ضتء؟µؤ²îضµ £¨µ¥خ»£؛؟ث£© |
|
| 0 | 1 | 3 | 6 |
´ü ت | 1 | 4 | 3 | 4 | 5 | 3 |
£¨1£©صâإْرùئ·µؤئ½¾ùضتء؟±ب±ê×¼ضتء؟¶à»¹تاةظ£؟¶à»ٍةظ¼¸؟ث£؟
£¨2£©بô±ê×¼ضتء؟خھ450؟ث£¬شٍ³éرù¼ى²âµؤ20´üت³ئ·µؤ×ـضتء؟خھ¶àةظ؟ث£؟
£¨3£©بô¸أضضت³ئ·µؤ؛د¸ٌ±ê×¼خھ450،ہ5؟ث£¬اَ¸أت³ئ·µؤ³éرù¼ى²âµؤ؛د¸ٌآت£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ضذر§خھ´ٍشىتéدمذ£ش°£¬¼ئ»®¹؛½ّ¼×،¢ززء½ضض¹و¸ٌµؤتé¹ٌ·إضأذآ¹؛½ّµؤح¼ت飬µ÷²é·¢دض£¬بô¹؛آٍ¼×ضضتé¹ٌ3¸ِ،¢ززضضتé¹ٌ2¸ِ£¬¹²ذè×ت½ً1020شھ£»بô¹؛آٍ¼×ضضتé¹ٌ4¸ِ£¬ززضضتé¹ٌ3¸ِ£¬¹²ذè×ت½ً1440شھ£®
£¨1£©¼×،¢ززء½ضضتé¹ٌأ؟¸ِµؤ¼غ¸ٌ·ض±ًتا¶àةظشھ£؟
£¨2£©بô¸أذ£¼ئ»®¹؛½ّصâء½ضض¹و¸ٌµؤتé¹ٌ¹²20¸ِ£¬ئنضذززضضتé¹ٌµؤتء؟²»ةظسع¼×ضضتé¹ٌµؤتء؟£¬ر§ذ£ضء¶àؤـ¹»جل¹©×ت½ً4320شھ£¬اëةè¼ئ¼¸ضض¹؛آٍ·½°¸¹©صâ¸ِر§ذ£ر،شٌ£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟خزأا¶¨زه:بç¹ûز»¸ِب½اذخز»جُ±كةدµؤ¸كµبسعصâجُ±ك,ؤاأ´صâ¸ِب½اذخ½ذ×ِ،°µب¸كµ×،±ب½اذخ,صâجُ±ك½ذ×ِصâ¸ِب½اذخµؤ،°µبµ×،±،£
£¨1£©¸إؤîہي½â:
بçح¼1,شع![]() ضذ,
ضذ,![]() ,
,![]() .
.![]() ,تشإذ¶د
,تشإذ¶د![]() تا·ٌتا،°µب¸كµ×،±ب½اذخ£¬اëثµأ÷ہيسة.
تا·ٌتا،°µب¸كµ×،±ب½اذخ£¬اëثµأ÷ہيسة.
£¨2£©ختجâج½¾؟:
بçح¼2, ![]() تا،°µب¸كµ×،±ب½اذخ,
تا،°µب¸كµ×،±ب½اذخ,![]() تا،°µبµ×،±£¬×÷
تا،°µبµ×،±£¬×÷![]() ¹طسع
¹طسع![]() ثùشعض±دكµؤ¶ش³ئح¼ذخµأµ½
ثùشعض±دكµؤ¶ش³ئح¼ذخµأµ½![]() ,ء¬½ل
,ء¬½ل![]() ½»ض±دك
½»ض±دك![]() سعµم
سعµم![]() .بôµم
.بôµم![]() تا
تا![]() µؤضطذؤ,اَ
µؤضطذؤ,اَ![]() µؤضµ.
µؤضµ.
£¨3£©س¦سأحطص¹:
بçح¼3,زرضھ![]() ,
,![]() سë
سë![]() ض®¼نµؤ¾àہëخھ2.،°µب¸كµ×،±
ض®¼نµؤ¾àہëخھ2.،°µب¸كµ×،±![]() µؤ،°µبµ×،±
µؤ،°µبµ×،± ![]() شعض±دك
شعض±دك![]() ةد,µم
ةد,µم![]() شعض±دك
شعض±دك![]() ةد
ةد![]() µؤ
µؤ![]() ±¶.½«
±¶.½«![]() بئµم
بئµم![]() °´ث³ت±صë·½دٍذ×ھ
°´ث³ت±صë·½دٍذ×ھ![]() µأµ½
µأµ½![]() ,
,![]() ثùشعض±دك½»
ثùشعض±دك½»![]() سعµم
سعµم![]() .اَ
.اَ![]() µؤضµ.
µؤضµ.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬´َآ¥ABسز²àسذز»صد°خشعصد°خïµؤإش±كسذز»´±ذ،آ¥DE£¬شعذ،آ¥µؤ¶¥¶ثD´¦²âµأصد°خï±كشµµمCµؤ¸©½اخھ30،م£¬²âµأ´َآ¥¶¥¶ثAµؤرِ½اخھ45،م£¨µمB£¬C£¬Eشعح¬ز»ث®ئ½ض±دكةد£©£¬زرضھAB=80 m£¬DE=10 m£¬اَصد°خïB£¬Cء½µم¼نµؤ¾àہ룮(½ل¹û¾«ب·µ½0.1 m)£¨²خ؟¼ت¾ف£؛ ![]() ،ض1.414£¬،¢
،ض1.414£¬،¢![]() ،ض1.732£©
،ض1.732£©

²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com