练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．解方程
    （1）$\frac{3x-5}{x-2}$=2+$\frac{x+1}{2-x}$                     
    （2）$\frac{2}{3}$+$\frac{x}{3x-1}$=$\frac{1}{9x-3}$．

    分析 两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

    解答 解：（1）去分母得：3x-5=2x-4-x-1，
    解得：x=0，
    经检验x=0是分式方程的解；
    （2）去分母得：6x-2+3x=1，
    解得：x=$\frac{1}{3}$，
    经检验x=$\frac{1}{3}$是增根，分式方程无解．

    点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．化简$\frac{2x}{{x}^{2}+2x}$-$\frac{x-6}{{x}^{2}-4}$的结果为（　　）
    A．$\frac{1}{{x}^{2}-4}$B．$\frac{1}{{x}^{2}+2x}$C．$\frac{1}{x-2}$D．$\frac{x-6}{x-2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知正方形ABCD和正方形AMNG，E、F分别是AD和AB的中点．

    （1）尝试探究：
    直接写出EG与FM的数量和位置关系；
    （2）类比延伸：
    正方形AMNG绕A点逆时针旋转90°之后，连接DG、EG、FM、BM，猜想EG与FM的数量和位置关系，试说明理由；
    （3）拓展迁移：
    正方形AMNG绕A点逆时针旋转α°（0＜α＜180）之后，连接DG、EG、FM、BM，猜想EG与FM的数量和位置关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列说法中，正确的是（　　）
    A．两条直线被第三条直线所截，同位角相等
    B．联结直线外一点到直线上各点的所有线段中，垂线最短
    C．经过一点，有且只有一条直线与已知直线平行
    D．在同一平面内，经过一点，有且只有一条直线与已知直线垂直

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．利用幂的运算性质计算：2$\root{6}{{4}^{2}}$×$\sqrt{8}$÷$\root{6}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．计算：$\frac{2}{{\sqrt{2}-1}}-\sqrt{8}$=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

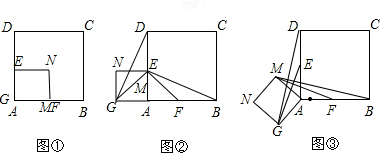
    9．已知：如图，等腰△ABC中，AB=AC，BD、CE分别是边AC、AB上的中线，BD与CE相交于点O，点M、N分别为线段BO和CO中点．求证：四边形EDNM是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，已知点A是直线y=2x+1与反比例函数y=$\frac{k}{x}$（x＞0）图象的交点，且点A的横坐标为1．

    （1）求k的值；
    （2）如图1，双曲线y=$\frac{k}{x}$（x＞0）上一点M，若S△AOM=4，求点M的坐标；
    （3）如图2所示，若已知反比例函数y=$\frac{k}{x}$（x＞0）图象上一点B（3，1），点P是直线y=x上一动点，点Q是反比例函数y=$\frac{k}{x}$（x＞0）图象上另一点，是否存在以P、A、B、Q为顶点的平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

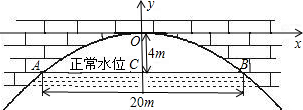    7．如图，有一抛物线形拱桥，正常水位时桥下水面宽20m，拱顶距离水面4m．已知其抛物线解析式为y=-0.04x2，在正常水位时，桥下的水深为2m，为保证过往船只顺利通行，桥下水面的宽度不得小于18m，求水深超过多少米时，就会影响过往船只从桥下顺利通行？

    查看答案和解析>>

    同步练习册答案