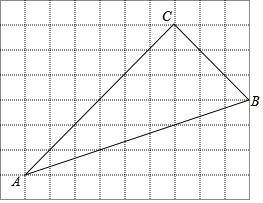
【题目】如图，在边长为1个单位长度的小正方形组成的8×10网格中，点A，B，C均为网格线的交点．
（1）用无刻度的直尺作BC边上的中线AD（不写作法，保留作图痕迹）；
（2）①在给定的网格中，以A为位似中心将△ABC缩小为原来的
，得到△AB′C′，请画出△AB′C′．
②填空：tan∠AD′C'＝ ．
科目：初中数学 来源： 题型：
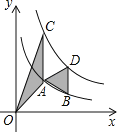
【题目】如图，点A，B在反比例函数y＝
(x＞0)的图象上，点C，D在反比例函数y＝
(k＞0)的图象上，AC∥BD∥y轴，已知点A，B的横坐标分别为1，2，△OAC与△ABD的面积之和为
，则k的值为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
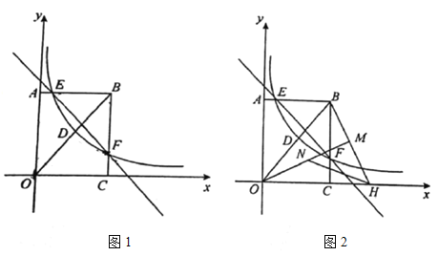
【题目】如图1，在矩形
中，
，分别以
所在的直线为
轴、
轴，建立如图所示的平面直角坐标系，连接
,反比例函数
的图象经过线段的中点
，并与矩形的两边交于点
和点
，直线
经过点和点.
（1）连接
、
，求
的面积；
（2）如图2，将线段绕点
顺时针旋转—定角度，使得点
的对应点
好落在轴的正半轴上，连接
，作
，点
为线段
上的一个动点，求
的最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
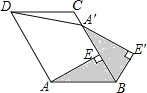
【题目】如图，已知平行四边形ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=50°，则∠DA′E′的度数为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况，从七、八年级各随机抽取50名学生进行测试，并对成绩（百分制）进行整理、描述和分析．部分信息如下：
a．七年级成绩频数分布直方图：
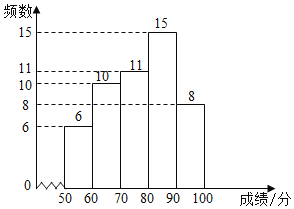
b．七年级成绩在
这一组的是：70 72 74 75 76 76 77 77 77 78 79
c．七、八年级成绩的平均数、中位数如下：
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息，回答下列问题：
（1）在这次测试中，七年级在80分以上（含80分）的有 人；
（2）表中m的值为 ；
（3）在这次测试中，七年级学生甲与八年级学生乙的成绩都是78分，请判断两位学生在各自年级的排名谁更靠前，并说明理由；
（4）该校七年级学生有400人，假设全部参加此次测试，请估计七年级成绩超过平均数76.9分的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：小胖同学遇到这样一个问题，如图1，在△ABC中，∠ABC＝45°，AB＝2
，AD＝AE，∠DAE＝90°，CE＝
，求CD的长；
小胖经过思考后，在CD上取点F使得∠DEF＝∠ADB（如图2），进而得到∠EFD＝45°，试图构建“一线三等角”图形解决问题，于是他继续分析，又意外发现△CEF∽△CDE．
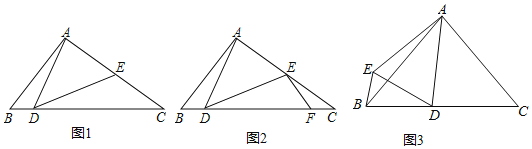
（1）请按照小胖的思路完成这个题目的解答过程．
（2）参考小胖的解题思路解决下面的问题：
如图3，在△ABC中，∠ACB＝∠DAC＝∠ABC，AD＝AE，
∠EAD+∠EBD＝90°，求BE：ED．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知平面直角坐标系
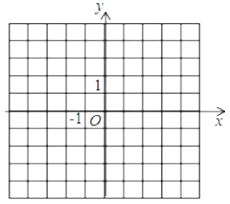
（1）请在图中用描点法画出二次函数y=－
x2+2x+1的图象；
（2）计算图象与坐标轴的交点，顶点坐标，写出对称轴；
（3）指出当x≤－3时，y随x的增大而增大还是y随x的增大而减少；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
