
【题目】如图1,在矩形![]() 中,
中,![]() ,分别以
,分别以![]() 所在的直线为
所在的直线为![]() 轴、
轴、![]() 轴,建立如图所示的平面直角坐标系,连接
轴,建立如图所示的平面直角坐标系,连接![]() ,反比例函数
,反比例函数![]() 的图象经过线段
的图象经过线段![]() 的中点
的中点![]() ,并与矩形的两边交于点
,并与矩形的两边交于点![]() 和点
和点![]() ,直线
,直线![]() 经过点
经过点![]() 和点
和点![]() .
.
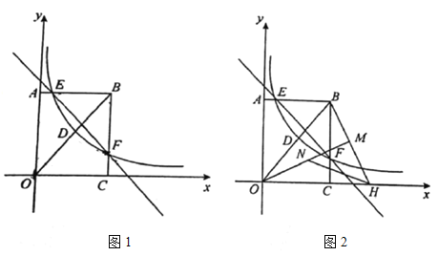
(1)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(2)如图2,将线段![]() 绕点
绕点![]() 顺时针旋转—定角度,使得点
顺时针旋转—定角度,使得点![]() 的对应点
的对应点![]() 好落在
好落在![]() 轴的正半轴上,连接
轴的正半轴上,连接![]() ,作
,作![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,求
上的一个动点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)4.
;(2)4.
【解析】
(1)连接![]() 、
、![]() ,过点D作DP⊥OC,易得:B(3,4),从而得D(1.5,2),进而得
,过点D作DP⊥OC,易得:B(3,4),从而得D(1.5,2),进而得![]() ,即:
,即:![]() ,E(
,E(![]() ,4),F(3,1),根据割补法,即可求出答案;
,4),F(3,1),根据割补法,即可求出答案;
(2)过点N作NQ⊥OB于点Q,HG⊥OB于点G,易得OH=OB=5,BH=![]() ,HG=BC=4,易证OQN~OMB,得NQ=
,HG=BC=4,易证OQN~OMB,得NQ=![]() ,得到
,得到![]() ,进而得到答案.
,进而得到答案.
(1)连接![]() 、
、![]() ,过点D作DP⊥OC,如图1,
,过点D作DP⊥OC,如图1,
∵在矩形![]() 中,
中,![]() ,
,
∴B(3,4),
∵点D是OB的中点,
∴DP=![]() BC=
BC=![]() OA=2,OP=
OA=2,OP=![]() OC=1.5,即:D(1.5,2),
OC=1.5,即:D(1.5,2),
∵反比例函数![]() 的图象经过线段
的图象经过线段![]() 的中点
的中点![]() ,
,
∴k=xy=1.5×2=3,即:![]() ,
,
∴![]() ,E(
,E(![]() ,4),F(3,1),
,4),F(3,1),
∴BE=3-![]() =
=![]() ,BF=4-1=3,
,BF=4-1=3,
∴![]() ,
,
∴![]() =
=![]()
![]() ;
;
(2)过点N作NQ⊥OB于点Q,HG⊥OB于点G,如图2,
∵线段![]() 绕点
绕点![]() 顺时针旋转—定角度,点
顺时针旋转—定角度,点![]() 的对应点
的对应点![]() 好落在
好落在![]() 轴的正半轴上,
轴的正半轴上,
∴OH=OB=![]() ,
,
∴CH= OH-OC=5-3=2,
∴BH=![]() ,
,
∵![]() ,
,
∴HG=BC=4,
∵![]() ,
,
∴BM=![]() BH=
BH=![]() ,
,
∵∠NOQ=∠BOM,∠OQN=∠OMB=90°,
∴OQN~OMB,
∴![]() ,即:
,即:![]() ,
,
∴NQ=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 的最小值是:4.
的最小值是:4.


科目:初中数学 来源: 题型:
【题目】抛物线y=x2+(2t﹣2)x+t2﹣2t﹣3与x轴交于A、B两点(A在B左侧),与y轴交于点C.
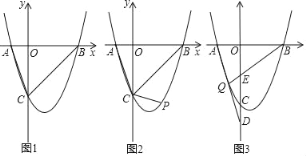
(1)如图1,当t=0时,连接AC、BC,求△ABC的面积;
(2)如图2,在(1)的条件下,若点P为在第四象限的抛物线上的一点,且∠PCB+∠CAB=135°,求P点坐标;
(3)如图3,当﹣1<t<3时,若Q是抛物线上A、C之间的一点(不与A、C重合),直线QA、QB分别交y轴于D、E两点.在Q点运动过程中,是否存在固定的t值,使得CE=2CD.若存在,求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有一露天舞台,纵断面如图所示,AC垂直于地面,AB表示楼梯,AE为舞台面,楼梯的坡角∠ABC=45°,坡长AB=2m,为保障安全,学校决定对该楼梯进行改造,降低坡度,拟修新楼梯AD,使∠ADC=30°
(1)求舞台的高AC(结果保留根号)
(2)楼梯口B左侧正前方距离舞台底部C点3m处的文化墙PM是否要拆除?请说明理由.
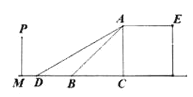
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校自主开发了A书法、B阅读,C绘画,D器乐四门选修课程供学生选择,每门课程被选到的机会均等.
(1)若学生小玲计划选修两门课程,请写出她所有可能的选法;
(2)若学生小强和小明各计划选修一门课程,则他们两人恰好选修同一门课程的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
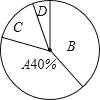
【题目】某校举行九年级体育锻炼考试,现随机抽取了部分学生的成绩为样本,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面两图不完整的统计图和统计表:
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 45~50 | 40 | 0.4 |
B | 40~44 | 42 | x |
C | 35~39 | m | 0.12 |
D | 30~34 | 6 | 0.03 |
合计 | 1.00 |
请根据以如图表提供的信息,解答下列问题:
(1)m= ,x= ;
(2)在扇形统计图中,B等级所对应的圆心角是 度;
(3)若该校九年级共有600名学生参加了体育模板考试,请你估计成绩等级达到“优秀”的学生有 人;
(4)小明同学第一次模拟考试成绩为40分,第二次成绩为48分,则小明体育成绩提高的百分率是 %.
查看答案和解析>>
科目:初中数学 来源: 题型:
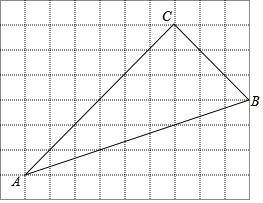
【题目】如图,在边长为1个单位长度的小正方形组成的8×10网格中,点A,B,C均为网格线的交点.
(1)用无刻度的直尺作BC边上的中线AD(不写作法,保留作图痕迹);
(2)①在给定的网格中,以A为位似中心将△ABC缩小为原来的![]() ,得到△AB′C′,请画出△AB′C′.
,得到△AB′C′,请画出△AB′C′.
②填空:tan∠AD′C'= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标和该抛物线的顶点坐标;
的坐标和该抛物线的顶点坐标;
(2)若该抛物线与![]() 轴交于
轴交于![]() 两点,求
两点,求![]() 的面积
的面积![]() ;
;
(3)将该抛物线先向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,求平移后的抛物线的解析式(直接写出结果即可).
个单位长度,求平移后的抛物线的解析式(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图:
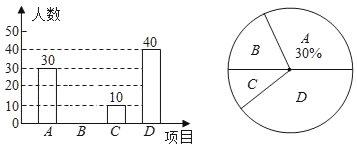
请结合图中所给信息,解答下列问题
(1)本次调查的学生共有 人;
(2)补全条形统计图;
(3)七年级一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有若千间标准客房,当房价为200元/间时,日均入住数为60间.市场调查表明,在物价局核定的每间标准房价格在160~220元之间(含160元,220元)浮动时,每提高10元,日均入住数减少10间.在不考虑其他因素的前提下,设标准房的价格为x元/间,日均入住数为y间. .
(1) y关于x的解析式为_ .
(2)当标准房的价格定为多少元时,客房的日营业额为10500元?
(3)当标准房的价格定为多少元时,客房的日营业额最大,最大为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com