
【题目】阅读材料:小胖同学遇到这样一个问题,如图1,在△ABC中,∠ABC=45°,AB=2![]() ,AD=AE,∠DAE=90°,CE=
,AD=AE,∠DAE=90°,CE=![]() ,求CD的长;
,求CD的长;
小胖经过思考后,在CD上取点F使得∠DEF=∠ADB(如图2),进而得到∠EFD=45°,试图构建“一线三等角”图形解决问题,于是他继续分析,又意外发现△CEF∽△CDE.
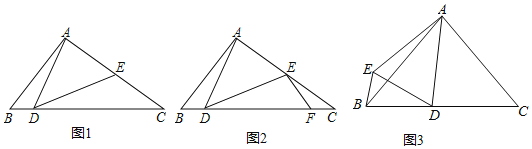
(1)请按照小胖的思路完成这个题目的解答过程.
(2)参考小胖的解题思路解决下面的问题:
如图3,在△ABC中,∠ACB=∠DAC=∠ABC,AD=AE,![]() ∠EAD+∠EBD=90°,求BE:ED.
∠EAD+∠EBD=90°,求BE:ED.
【答案】CD=5;(1)见解析;(2)![]()
【解析】
(1)在CD上取点F,使∠DEF=∠ADB,证明△ADB∽△DEF,求出DF=4,证明△CEF∽△CDE,由比例线段可求出CF=1,则CD可求出;
(2)如图3,作∠DAT=∠BDE,作∠RAT=∠DAE,通过证明△DBE∽△ATD,可得![]() ,可得
,可得 ![]() ,通过证明△ARE≌△ATD,△ABR≌△ACT,可得BR=TC=DT,即可求解.
,通过证明△ARE≌△ATD,△ABR≌△ACT,可得BR=TC=DT,即可求解.
解:(1)在CD上取点F,使∠DEF=∠ADB,
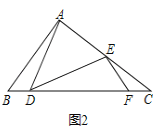
∵AD=AE,∠DAE=90°,
∴DE=![]() AD=
AD=![]() AE,
AE,
∵∠ABC=45°,∠ADE=45°,
且∠ADC=∠ADE+∠EDC,
∴∠BAD=∠EDC,
∵∠BDA=∠DEF,
∴△ADB∽△DEF,
∴![]() =
=![]() ,
,
∵AB=2![]() ,
,
∴DF=4,
又∵∠CDE+∠C=45°,
∴∠CEF=∠CDE,
∴△CEF∽△CDE,
∴![]() ,
,
又∵DF=4,CE=![]() ,
,
∴![]() ,
,
∴CF=1或CF=5(舍去),
∴CD=CF+4=5;
(2)如图3,作∠DAT=∠BDE,作∠RAT=∠DAE,
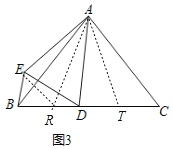
∵∠ACB=∠DAC=∠ABC,
∴AB=AC,AD=CD,
∵AD=AE,
∴∠AED=∠ADE,
∵![]() ∠EAD+∠EBD=90°,
∠EAD+∠EBD=90°,
∴∠EAD+2∠EBD=180°,且∠EAD+2∠AED=180°,
∴∠EBD=∠AED=∠ADE,
∵∠BDA=∠DAT+∠ATD=∠BDE+∠ADE,
∴∠ADE=∠ATD=∠EBD,且∠BDE=∠DAT,
∴△DBE∽△ATD,
∴![]() ,∠ADT=∠BED,
,∠ADT=∠BED,
∴![]() ,且AD=DC,
,且AD=DC,
∴![]() ,
,
∵∠RAT=∠DAE,∠ADE=∠ATD,
∴∠RAE=∠DAT,∠AED=∠ART=∠ADE=∠ATD,
∴AR=AT,且∠RAE=∠DAT,∠ARE=∠ATD,
∴△ARE≌△ATD(ASA)
∴∠ADT=∠AER,DT=ER,
∴∠BED=∠AER,
∴∠AED=∠BER=∠EBD,
∴RE=RB=DT,
∵AB=AC,∠ABC=∠ACB,∠ARB=∠ATC,
∴△ABR≌△ACT(AAS)
∴BR=TC,
∴DT=TC,
∴CD=2DT,
∴![]() =
=![]()


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
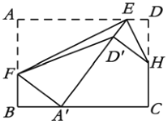
【题目】如图,矩形纸片![]() 中,
中,![]() ,
,![]() ,将纸片沿
,将纸片沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,折痕分别交边
处,折痕分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() .再将纸片沿
.再将纸片沿![]() 折叠,使点
折叠,使点![]() 落在线段
落在线段![]() 上的
上的![]() 处,折痕交边
处,折痕交边![]() 于点
于点![]() .连接
.连接![]() ,则
,则![]() 的长是______
的长是______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
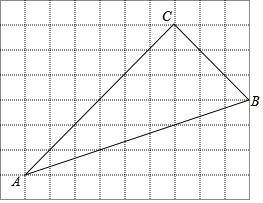
【题目】如图,在边长为1个单位长度的小正方形组成的8×10网格中,点A,B,C均为网格线的交点.
(1)用无刻度的直尺作BC边上的中线AD(不写作法,保留作图痕迹);
(2)①在给定的网格中,以A为位似中心将△ABC缩小为原来的![]() ,得到△AB′C′,请画出△AB′C′.
,得到△AB′C′,请画出△AB′C′.
②填空:tan∠AD′C'= .
查看答案和解析>>
科目:初中数学 来源: 题型:
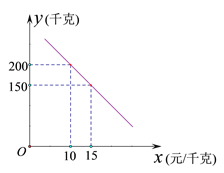
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间的函数关系如图所示.
(元/千克)之间的函数关系如图所示.
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图:
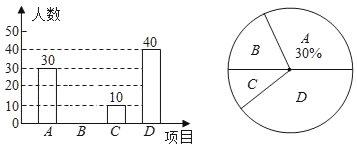
请结合图中所给信息,解答下列问题
(1)本次调查的学生共有 人;
(2)补全条形统计图;
(3)七年级一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元.市场调査发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量![]() (箱)与销售价
(箱)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:![]() 记为
记为![]() ,它与
,它与![]() 轴交于两点
轴交于两点![]() ,
,![]() ;将
;将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() ;将
;将![]() 绕
绕![]() 旋转
旋转![]() 得到
得到![]() ,交
,交![]() 轴于
轴于![]() ;…如此进行下去,直至得到
;…如此进行下去,直至得到![]() ,若点
,若点![]() 在第6段抛物线
在第6段抛物线![]() 上,则
上,则![]() ______.
______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com