
【题目】(1)如图1,已知![]() ,
,![]() ,可得
,可得![]() =______;
=______;
(2)如图2,在(1)的条件下,如果![]() 平分
平分![]() ,则
,则![]() =________;
=________;
(3)如图3,在(1)(2)的条件下,如果![]() ,则
,则![]() =_________;
=_________;
(4)尝试解决下面问题:如图4,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,求
,求![]() 的度数.
的度数.




【答案】 60° 30° 60°
【解析】分析:(1)∠BCD与∠ABC是两平行直线AB、CD被BC所截得到的内错角,所以根据两直线平行,内错角相等即可求解;
(2)根据角平分线的定义求解即可;
(3)根据互余的两个角的和等于90°,计算即可;
(4)先根据两直线平行,同旁内角互补和角平分线的定义求出∠BCN的度数,再利用互余的两个角的和等于90°即可求出.
详解:(1)∵AB//CD,∴∠BCD=∠B=60°.
故答案为:60°;
(2)∵CM平分∠BCD,∴∠BCN=![]() ∠BCD=
∠BCD=![]() ×60°=30°.
×60°=30°.
故答案为:30°;
(3)∵CN⊥CM,∴∠MCN=90°,∴∠BCN=90°-∠BCM=90°-30°=60°.故答案为:60°;
(4)∵AB∥CD,∴∠B+∠BCE=180°.
∵∠B=40°,∴∠BCE=180°﹣∠B=180°﹣40°=140°.
又∵CN是∠BCE的平分线,∴∠BCN=140°÷2=70°.
∵CN⊥CM,∴∠BCM=90°﹣∠BCN=90°﹣70°=20°.


科目:初中数学 来源: 题型:
【题目】完成下面的证明(在下面的括号内填上相应的结论或推理的依据):如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,
求证:AD是∠BAC的平分线.

证明:∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°( )
∴AD∥EG( )
∴∠1=∠E( ) ∠2=∠3( )
∵∠E=∠3(已知)
∴( )=( )
∴AD是∠BAC的平分线( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭绍台高铁项目是国内首批八个社会资本投资铁路示范项目之一,也是中国首个民营控股高速铁路项目.该项目可用批复总投资预计448.9亿元,资本金占总投资的30%,其中民营联合体占股51%,其中448.9亿元用科学记数法表示为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
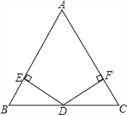
【题目】如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;
(2)若∠A=![]() ,BE=5.
,BE=5.
①求证: ![]() ②求△ABC的周长.
②求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2 018次运动后,动点P的坐标是( )

A. (2018,0) B. (2018,1) C. (2018,2) D. (2017,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
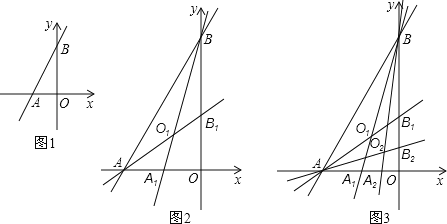
【题目】如图1,一次函数y=2x+4与x轴,y轴分别相交于A,B两点,一次函数图象与坐标轴围成的△ABO,我们称它为此一次函数的坐标三角形.把坐标三角形面积分成相等的二部分的直线叫做坐标三角形的等积线.
(1)求此一次函数的坐标三角形周长以及过点A的等积线的函数表达式;
(2)如图2,我们把第一个坐标三角形△ABO记为第一代坐标三角形.第一代坐标三角形的等积线BA1,AB1记为第一对等积线,它们交于点O1,四边形A1OB1O1称为第一个坐标四边形.求点O1的坐标和坐标四边形A1OB1O1面积;
(3)如图3.第一对等积线与坐标轴构成了第二代坐标三角形△BA1O.△AOB1分别过点A,B作一条平分△BA1O,△AOB1面积的第二对等积线BA2,AB2,相交于点O2,如此进行下去.…,请直接写出On的坐标和第n个坐标四边形面积(用n表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°. 
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出定义:设一条直线与一条抛物线只有一个公共点,且这条直线与这条抛物线的对称轴不平行,就称直线与抛物线相切,这条直线是抛物线的切线.有下列命题: ①直线y=0是抛物线y= ![]() x2的切线;
x2的切线;
②直线x=﹣2与抛物线y= ![]() x2 相切于点(﹣2,1);
x2 相切于点(﹣2,1);
③若直线y=x+b与抛物线y= ![]() x2相切,则相切于点(2,1);
x2相切,则相切于点(2,1);
④若直线y=kx﹣2与抛物线y= ![]() x2相切,则实数k=
x2相切,则实数k= ![]() .
.
其中正确命题的是( )
A.①②④
B.①③
C.②③
D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com