
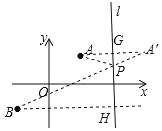
【题目】定义:如图1,A,B为直线l同侧的两点,过点A作直线l的对称点A′,连接A′B交直线于点P,连接AP,则称点P为点A,B关于直线l的“等角点”.
运用:如图2,在平面直坐标系xOy中,已知A(2,![]() ),B(﹣2,﹣
),B(﹣2,﹣![]() )两点
)两点
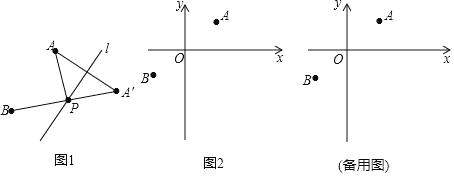
(1)C(4,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() ),哪个点是点A,B关于直线x=4的“等角点”;
),哪个点是点A,B关于直线x=4的“等角点”;
(2)若直线l垂直于x轴,点P(m,n)是点A,B关于直线l的“等角点”,其中m>2,∠APB=α,求证:tan![]() .
.
【答案】(1)点C;(2)见解析
【解析】
(1)点B关于直线x=4的对称点为B′(10,![]() ),由待定系数法求出直线AB′的解析式为y=﹣
),由待定系数法求出直线AB′的解析式为y=﹣![]() x+
x+![]() ,当x=4时,y=
,当x=4时,y=![]() ,即可得出结果;
,即可得出结果;
(2)过点A作直线l的对称点A′,连接A′B,交直线l于点P,作BH⊥l于点H,由点A和A′关于直线l对称,得出∠APG=∠A′PG,证明△AGP∽△BHP,得出![]() =
=![]() ,求出m=
,求出m=![]() ,由∠APB=α,AP=A′P,得出∠A=∠A′=
,由∠APB=α,AP=A′P,得出∠A=∠A′=![]() ,在Rt△AGP中,tan
,在Rt△AGP中,tan![]() =
=![]() =
=![]() =
=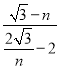 =
=![]() .
.
(1)解:点B关于直线x=4的对称点为B′(10,﹣![]() ),
),
设直线AB′的解析式为:y=kx+b,
则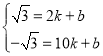 ,
,
解得: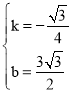 ,
,
∴直线AB′的解析式为:y=﹣![]() x+
x+![]() ,
,
当x=4时,y=![]() ,
,
∴点C(4,![]() )是点A,B关于直线x=4的“等角点”;
)是点A,B关于直线x=4的“等角点”;
(
∵点A和A′关于直线l对称,
∴∠APG=∠A′PG,
∵∠BPH=∠A′PG,
∴∠APG=∠BPH,
∵∠AGP=∠BHP=90°,
∴△AGP∽△BHP,
∴![]() =
=![]() ,
,
即:![]() =
=![]() ,
,
∴mn=2![]() ,
,
∴m=![]() ,
,
∵∠APB=α,AP=A′P,
∴∠A=∠A′=![]() ,
,
在Rt△AGP中,tan![]() =
=![]() =
=![]() =
=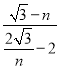 =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】在△ABC,∠ACB=90°,∠ABC=30°,将△ABC 绕顶点 C 顺时针旋转,旋转角为0 180 ,得到 ABC
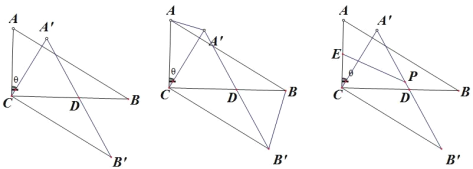
(1)求当角为多少度时, CBD 是等腰三角形;
(2)如图②,连接 AA, BB ,设 ACA , BCB 的面积分别为 S1 , S2 ,求![]() 的值;
的值;
(3)如图③,设 AC 的中点为 E, AB 的中点为 P,AC=a,连接 EP,当旋转角为多少时,EP 长度最大,并求出 EP 的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )
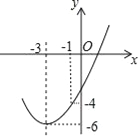
A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像过点A(1,2),B(3,2),C(5,7).若点M(-2,
的图像过点A(1,2),B(3,2),C(5,7).若点M(-2,![]() ),N(-1,
),N(-1,![]() ),K(8,
),K(8,![]() )也在二次函数
)也在二次函数![]() 的图像上,则
的图像上,则![]() ,
,![]() ,
,![]() 的从小到大的关系是 .
的从小到大的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日上午7:00,一列火车在A城的正北24km处,以12km/h的速度驶向A城.同时,一辆汽车在A城的正东12km处,以12km/h的速度驶向正西方向行驶.假设火车和汽车的行驶的方向和速度都保持不变.
问:(1)何时火车与汽车之间的距离最近?最近距离是多少千米?
(2)当火车与汽车之间的距离最近时,汽车是否已过铁路与公路的立交处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,分别过点A,C作AE∥DC,CE∥AB,两线交于点E.
(1)求证:四边形AECD是菱形;
(2)如果∠B=60°,BC=2,求四边形AECD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com