
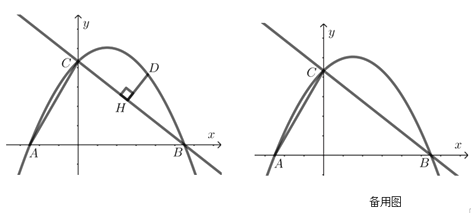
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线![]() 经过点B和点C,且与x轴交于另一点A,连接AC,点D在BC上方的抛物线上,设点D的横坐标为m,过点D作DH⊥BC于点H.
经过点B和点C,且与x轴交于另一点A,连接AC,点D在BC上方的抛物线上,设点D的横坐标为m,过点D作DH⊥BC于点H.
(1)求抛物线的函数表达式;
(2)线段DH的长为 (用含m的代数式表示);
(3)点M为线段AC上一点,连接OM绕点O顺时针旋转60°得线段ON,连接CN,当CN=![]() ,m=6时,请直接写出此时线段DM的长.
,m=6时,请直接写出此时线段DM的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)利用待定系数法即可求得解析式;
(2)利用勾股定理列方程计算即可得出;
(3)作∠NPO=60°(点P在x轴上),作NQ⊥x轴,交x轴于点Q,
作NH⊥y轴交y轴于点H,作MG⊥x轴交x轴于点G,交DS于点T,DS⊥x轴于点S,
做出辅助线后根据条件讨论即可.
(1)根据![]() 可得B(11,0),C(0,
可得B(11,0),C(0,![]() ),
),
将B,C两点代入![]() ,
,
得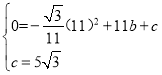 ,解得
,解得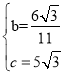 ,
,
∴解析式为:![]() ;
;
(2)由题意可得B(11,0),C(0,![]() ),
),
∴OB=11,OC=![]() ,
,
∵D点的横坐标为m,
∴D点的坐标可表示为(m,![]() )
)
∴|BC|=![]() ,
,
|DC|=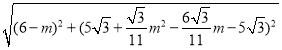 ,
,
|BD|=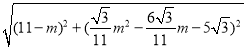 ,
,
设CH=x,
∴|DC|2-x2=|BD|2-(14-x)2
解得x=![]() ,
,
|DH|=![]() ;
;
(3))如图,作∠NPO=60°(点P在x轴上),作NQ⊥x轴,交x轴于点Q,
作NH⊥y轴交y轴于点H,作MG⊥x轴交x轴于点G,交DS于点T,DS⊥x轴于点S,

∵抛物线![]() 交x轴于点A,B,
交x轴于点A,B,
∴令![]()
解得x1=11,x2=-5,
即A(-5,0),OA=5,
∵tan=![]() ,
,
∴∠CAO=60°,∠ACO=30°,
∵∠MON=60°,∠CAO=120°,
∴∠MOA+∠NOP=120°,∠MOA+∠AMO=120°,
∴∠NOP=∠AMO,
在△MOA和△ONP中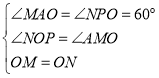 ,
,
∴△MOA≌△ONP(AAS),
∴NP=OA=5,
在Rt△NQP中,QP=NP·cos60°=![]() ,NQ=NP·sin60°=
,NQ=NP·sin60°=![]() ,
,
在四边形NHOQ中,∠NQO=∠QOP=∠OQN=90°,
∴∠HNQ=90°,
∴四边形NHOQ是矩形,
∴OH=NQ=![]() ,CH=OC-OH=
,CH=OC-OH=![]() -
-![]() =
=![]() ,
,
在Rt△CHN中,HN=![]() ,
,
在Rt△HNO中,ON=![]() ,
,
∴OM=ON=![]() ,
,
设MG=a,则GC=![]() =
=![]() ,OG=
,OG=![]() -
-![]() ,
,
在Rt△MOG中,DM2=MG2+OG2,
即212=a2+(![]() -
-![]() )2,整理得:(a-3)(2a-9)=0,
)2,整理得:(a-3)(2a-9)=0,
解得a1=3,a2=![]() ,
,
当m=6时,D(6,![]() ),
),
①a1=3时,MT=3+6=9,TS=OG=![]() ,DT=
,DT=![]() -
-![]() =
=![]() ,
,
在Rt△DMT中,DM=![]() ,
,
②a2=![]() 时,MT=
时,MT=![]() +6=
+6=![]() ,TS=OG=
,TS=OG=![]() ,DT=
,DT=![]() -
-![]() =
=![]() ,
,
在Rt△MDT中,DM=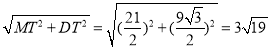 ,
,
综上DM的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),与
点的左侧),与![]() 轴相交于
轴相交于![]() 点,且
点,且![]() .
.

(1)求这条抛物线的解析式;
(2)如图2,![]() 点在
点在![]() 轴上,且在
轴上,且在![]() 点的右侧,
点的右侧,![]() 点为抛物线上第二象限内的点,连接
点为抛物线上第二象限内的点,连接![]() 交抛物线于第二象限内的另外一点
交抛物线于第二象限内的另外一点![]() ,点
,点![]() 到
到![]() 轴的距离与点
轴的距离与点![]() 到
到![]() 轴的距离之比为
轴的距离之比为![]() ,已知
,已知![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图3,在(2)的条件下,点![]() 由
由![]() 出发,沿
出发,沿![]() 轴负方向运动,连接
轴负方向运动,连接![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一条直线把一个平面图形分成面积相等的两部分,那么这条直线叫做该平面图形的“和谐线”,其“和谐线”被该平面图形截得的线段叫做该平面图形的“和谐线段”(例如圆的直径就是圆的“和谐线段”)
问题探究:
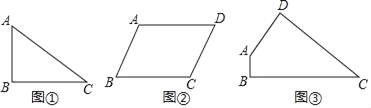
(1)如图①,已知△ABC中,AB=6,BC=8,∠B=90°,请写出△ABC的两条“和谐线段”的长.
(2)如图②,平行四边形ABCD中,AB=6,BC=8,∠B=60°,请直接写出该平行四边形ABCD的“和谐线段”长的最大值和最小值;
问题解决
(3)如图③,四边形ABCD是某市规划中的商业区示意图,其中AB=2,CD=10,∠A=135°,∠B=90°,tanC=![]() ,现计划在商业区内修一条笔直的单行道MN(小道的宽度不计),入口M在BC上,出口N在CD上,使得MN为四边形ABCD“和谐线段”,在道路一侧△MNC区域规划为公园,为了美观要求△MNC是以CM为腰的等腰三角形,请通过计算说明设计师的想法能否实现?若可以,请确定点M的位置(即求CM的长).
,现计划在商业区内修一条笔直的单行道MN(小道的宽度不计),入口M在BC上,出口N在CD上,使得MN为四边形ABCD“和谐线段”,在道路一侧△MNC区域规划为公园,为了美观要求△MNC是以CM为腰的等腰三角形,请通过计算说明设计师的想法能否实现?若可以,请确定点M的位置(即求CM的长).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其对称轴为直线
点,其对称轴为直线![]() .
.
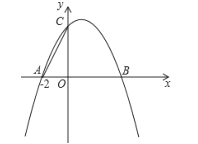
(1)直接写出抛物线的解析式;
(2)把线段![]() 沿
沿![]() 轴向右平移,设平移后
轴向右平移,设平移后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,当
,当![]() 落在抛物线上时,求
落在抛物线上时,求![]() 、
、![]() 的坐标;
的坐标;
(3)除(2)中的平行四边形![]() 外,在
外,在![]() 轴和抛物线上是否还分别存在点
轴和抛物线上是否还分别存在点![]() 、
、![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,求出
为顶点的四边形为平行四边形?若存在,求出![]() 、
、![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点E和点F是对角线AC上的两点,AF=CE,DF=BE,且DF∥BE,过点C作CG⊥AB交AB延长线与点G.
(1)求证:四边形ABCD是平行四边形;
(2)若tan∠CAB=![]() ,∠CBG=45°,BC=
,∠CBG=45°,BC=![]() ,则ABCD的面积是 .
,则ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是反比例函数
是反比例函数![]()
![]() 图象上的点,
图象上的点,![]() 于点
于点![]() ,
,![]() .
.
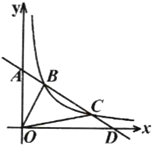
(1)求直线![]() 的函数解析式及反比例函数的解析式;
的函数解析式及反比例函数的解析式;
(2)若![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 的一个数量关系式.
的一个数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 、
、![]() 、
、![]() 在第二象限,横坐标分别是-4、-2、-1,双曲线
在第二象限,横坐标分别是-4、-2、-1,双曲线![]() 过
过![]() 、
、![]() 、
、![]() 三点,且
三点,且![]() .
.
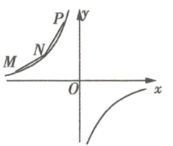
(1)求双曲线的解析式;
(2)过![]() 点的直线
点的直线![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,且
,且![]() ,且交
,且交![]() 于另一点
于另一点![]() ,求
,求![]() 点坐标;
点坐标;
(3)以![]() 为边(顺时针方向)作正方形
为边(顺时针方向)作正方形![]() ,平移正方形使
,平移正方形使![]() 落在
落在![]() 轴上,点
轴上,点![]() 、
、![]() 对应的点
对应的点![]() 、
、![]() 正好落在反比例函数
正好落在反比例函数![]() 上,求
上,求![]() 对应点
对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,若坡角∠FAE=30°,求大树的高度(结果保留根号).
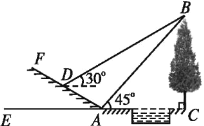
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点H,过CD的延长线上一点E作⊙O的切线交AB的延长线于点F,切点为点G,连接AG交CD于点K.
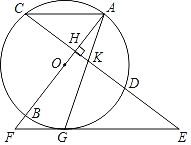
(1)求证:△EKG是等腰三角形;
(2)若KG2=KDGE,求证:AC∥EF;
(3)在(2)的条件下,若tanE=![]() ,AK=2
,AK=2![]() ,求FG的长.
,求FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com