
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点H,过CD的延长线上一点E作⊙O的切线交AB的延长线于点F,切点为点G,连接AG交CD于点K.
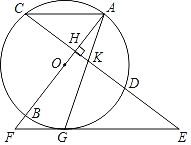
(1)求证:△EKG是等腰三角形;
(2)若KG2=KDGE,求证:AC∥EF;
(3)在(2)的条件下,若tanE=![]() ,AK=2
,AK=2![]() ,求FG的长.
,求FG的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接OG,证得∠KGE=∠AKH=∠GKE,可得KE=GE.则结论得证;
(2)连接GD,证明△GKD∽△EGK.得出∠E=∠AGD.则∠E=∠C,结论得证;
(3)连接OG,OC,设AH=3t,CH=4t,则AC=5t.由勾股定理得出(3t)2+t2=(2![]() )2,解得t=2,则AH=6,CH=8.⊙O的半径为r,在Rt△OCH中,OC=r,OH=r-6,CH=8,由勾股定理得出(r-6)2+82=r2,解得r=
)2,解得t=2,则AH=6,CH=8.⊙O的半径为r,在Rt△OCH中,OC=r,OH=r-6,CH=8,由勾股定理得出(r-6)2+82=r2,解得r=![]() .求出OG,可求出FG的长.
.求出OG,可求出FG的长.
(1)证明:如图1,连接OG,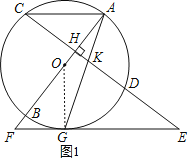
∵EG为⊙O的切线,
∴∠KGE+∠OGA=90°.
∵CD⊥AB,
∴∠AKH+∠OAG=90°.
又∵OA=OG,
∴∠OGA=∠OAG.
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
∴△EKG是等腰三角形.
(2)证明:如图2,连接GD,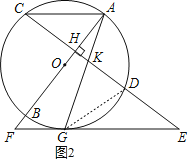
∵KG2=KDGE,
∴![]() .
.
又∵∠KGE=∠GKE,
∴△GKD∽△EGK.
∴∠E=∠AGD.
又∠C=∠AGD,
∴∠E=∠C.
∴AC∥EF.
(3)解:如图3,连接OG,OC,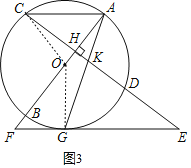
由tanE=tan∠ACH=![]() ,可设AH=3t,CH=4t,则AC=5t.
,可设AH=3t,CH=4t,则AC=5t.
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK-CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=(2![]() )2,
)2,
解得t=2或t=-2(不合题意,舍去).
∴AH=6,CH=8.
设⊙O的半径为r,在Rt△OCH中,OC=r,OH=r-6,CH=8,
由勾股定理得OH2+CH2=OC2,
即(r-6)2+82=r2,
解得r=![]() .
.
∵EF为⊙O的切线,
∴△OGF为直角三角形.
在Rt△OGF中,OG=r=![]() ,
,
∵tan∠OFG=tan∠CAH= ,
∴FG=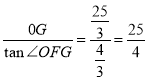 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
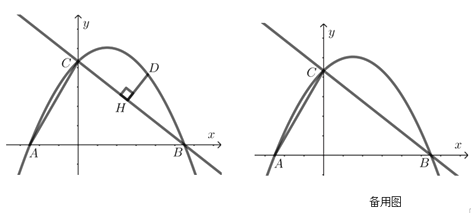
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线![]() 经过点B和点C,且与x轴交于另一点A,连接AC,点D在BC上方的抛物线上,设点D的横坐标为m,过点D作DH⊥BC于点H.
经过点B和点C,且与x轴交于另一点A,连接AC,点D在BC上方的抛物线上,设点D的横坐标为m,过点D作DH⊥BC于点H.
(1)求抛物线的函数表达式;
(2)线段DH的长为 (用含m的代数式表示);
(3)点M为线段AC上一点,连接OM绕点O顺时针旋转60°得线段ON,连接CN,当CN=![]() ,m=6时,请直接写出此时线段DM的长.
,m=6时,请直接写出此时线段DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
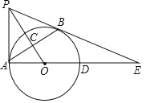
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=12cm,BC=16cm,AB=20cm,∠CAB的角平分线AD交BC于点D.
(1)根据题意将图形补画完整(要求:尺规作图保留作图痕迹,不写作法);
(2)求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
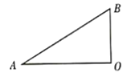
【题目】如图,![]() 是直角三角形,
是直角三角形,![]() .
.
(1)请用尺规作图法,作![]() ,使它与
,使它与![]() 相切于点
相切于点![]() ,与
,与![]() 相交于点
相交于点![]() ;保留作图痕迹,不写作法,请标明字母)
;保留作图痕迹,不写作法,请标明字母)
(2)在(1)的图中,若![]() ,
,![]() ,求弧
,求弧![]() 的长.(结果保留
的长.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
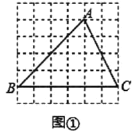
【题目】图①、图②、图③都是![]() 的网格,每个小正方形的顶点称为格点.
的网格,每个小正方形的顶点称为格点.![]() 顶点
顶点![]() 、
、![]() 、
、![]() 均在格点上,在图①、图②、图③给定网格中按要求作图,并保留作图痕迹.
均在格点上,在图①、图②、图③给定网格中按要求作图,并保留作图痕迹.
(1)在图①中画出![]() 中
中![]() 边上的中线
边上的中线![]() ;
;
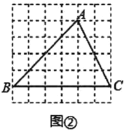
(2)在图②中确定一点![]() ,使得点
,使得点![]() 在
在![]() 边上,且满足
边上,且满足![]() ;
;
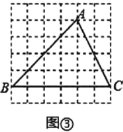
(3)在图③中画出![]() ,使得
,使得![]() 与
与![]() 是位似图形,且点
是位似图形,且点![]() 为位似中心,点
为位似中心,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上,位似比为
边上,位似比为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E且AB=AE,延长AB与DE的延长线相交于点F,连接AC、CF.下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③BF=AD;④S△BEF=S△ABC;⑤S△CEF=S△ABE;其中正确的有( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.
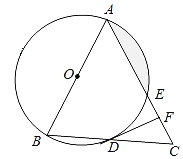
(1)求证:直线DF是⊙O的切线;
(2)求证:BC2=4CFAC;
(3)若⊙O的半径为2![]() ,∠CDF=15°,求阴影部分的面积.
,∠CDF=15°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
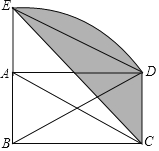
【题目】如图,在矩形ABCD中,AC、BD为对角线,AB=2,把BD绕点B逆时针旋转,得到线段BE,当点E落在线段BA的延长线时,恰有DE∥AC,连接CE,则阴影部分的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com