
����Ŀ����֪����EΪAB���ϵ�һ�����㣮
��1����ͼ1������ABC�ǵȱ������Σ���CEΪ����BC��ͬ�����ȱߡ�DEC������AD���ԱȽϡ�DAC���B�Ĵ�С����˵�����ɣ�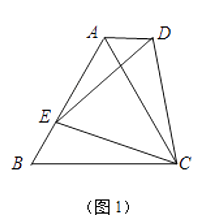
��2����ͼ2������ABC�У�AB=AC����CEΪ�ױ���BC��ͬ����������DEC���ҡ�DEC�ס�ABC������AD�����ж�AD��BC��λ�ù�ϵ����˵�����ɣ�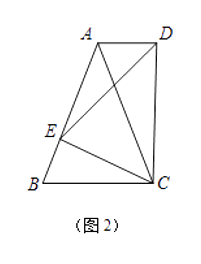
��3����ͼ3�����ı���ABCD�DZ߳�Ϊ2�������Σ���CEΪ����BC��ͬ����������ECGF��
����˵����Gһ����AD���ӳ����ϣ�
�ڵ���E��AB�����ɵ�B�˶�����Aʱ����F��֮�˶������F���˶�·������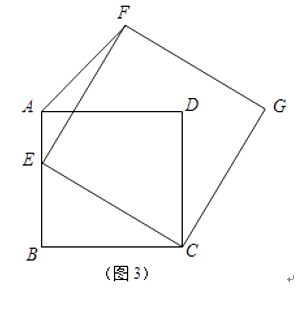
���𰸡�
��1���⣺��DAC=��B
�������£�
�ߡ�ABC�͡�DEC���ǵȱ�������
���DCE=��ACB=60��
���BCE=��ACD
�ڡ�BEC�͡�ADC�У�
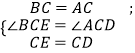
���BCE�ա�ACD��
���B=��DAC
��2���⣺AD��BC
�������£�
�ߡ�ABC�͡�DEC���ǵ��������Σ��ҡ�DEC�ס�ABC
�� ![]()
�ߡ�DCE=��ACB��
���DCA=��ECB��
���DCA�ס�ECB��
���DAC=��EBC=��ACB��
��AD��BC
��3���⣺������DG��
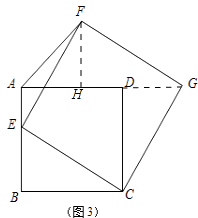
���ı���ABCD��FECG����������
��BC=CD��CE=CG����BCD=��ECG=90�㣮
���BCE=��DCG��
���BCE�ա�DCG��
���B=��CDG=90�㣮
�ߡ�ADC=90�㣮
���ADC+��CDG=180��
���Gһ����AD���ӳ����ϣ�
����FH��AG�ڵ�H��

�ߡ�BCE+ECD=90�㣬��ECD+DCG=90�㣬
���BCE=��GCD��
�ߡ�GCD+��CGD=90�㣬��CGD+��FGH=90��
���FGH=��GCD��
���BCE=��FGH=��GCD��
�ڡ�FHG�͡�GDC�͡�EBC�У�
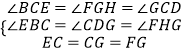 ��
��
���FHG�ա�GDC�ա�EBC��
��FH=BE=DG��HG=BC��
��AH=AG��GH=AD+DG��GH=BC+DG��BC=DG=FH��
���AFH�ǵ���ֱ�������Σ�
���FAG=45�㣮
���F���˶�·����=AC= ![]() =2
=2 ![]()
����������1���ɹ۲�����������ȣ���֤�������ڵ�������ȫ�ȣ�����BCE�ա�ACD���ó���B=��DAC����2����ȣ�1���ķ������۲�ͼ�Σ��ɲ����DEC�ס�ABC������֤����DCA�ס�ECB���ó���DAC=��EBC=��ACB��AD��BC����3�����о���ʼλ��A���ɡ�FHG�ա�GDC�ա�EBC���ɵá�AFH�ǵ���ֱ�������Σ�F���˶�����Ϊ����AD�н�Ϊ45�ȷ����ƶ����յ�ΪF����F���˶�·����=AC�����ù��ɶ������.
�����㾫����������Ĺؼ���������ɶ����ĸ�������֪ʶ������ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���Լ������������ε��ж������ʵ����⣬�˽����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��ı��� OABC �Ķ��� A��C �ֱ��� x ��� y ���ϣ�����B �ڵ�һ���ޣ�OA//CB��
��1����ͼ 1������ A(6��0)��B(4��3)���� M �� y ����һ�㣬�� SBCM SAOM ����� M�����ꣻ
��2����ͼ 2���� P �� x ���ϵ� A ��ߵ�һ�㣬���� PB����PBC �͡�PAB �Ľ�ƽ���߽��ڵ�D����֤����ABP+2��ADB=180����
��3����ͼ 3���� P �� x ���ϵ� A ��ߵ�һ�㣬�� Q ������ BC ��һ�㣬���� PB��PQ����ABP�͡�BQP ��ƽ�����ཻ�ڵ� E����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ʲô�ǡ���̼����𣿡���̼�����ָ���������о������������������Ӷ�����̼���ر��Ƕ�����̼�����ŷ�����һ�����ʽ��

��1�������x��L����ʾ����������y��kg����ʾ��˽�ҳ��Ķ�����̼�ŷ�������y��x֮��Ĺ�ϵʽ�ɱ�ʾΪ___________��
��2����������ϵʽ�У�������ÿ����1L��������̼�ŷ�������________kg������������10L���ӵ�100Lʱ��������̼�ŷ�����________kg���ӵ�________kg��
��3��Сӱ�ұ��¼Ҿ��õ�ĺĵ���ԼΪ90kwh����˽�ҳ��ĺ�����ԼΪ70L����Ȼ��ʹ����Լ20m������ˮʹ����Լ6�֣��������һ��Сӱ�ұ����⼸��Ķ�����̼�ŷ�������
��4����������ЩС��������е�̼�����ֱ��д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ����ABCD�У���E��F�ֱ���AD��BC���е㣬�ֱ�����BE��DF��BD��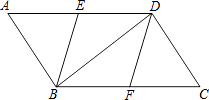
��1����֤����AEB�ա�CFD��
��2�����ı���EBFD�����Σ����ABD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E�DZ߳�Ϊ1��������ABCD�ı�AB������һ�㣨����A��B������B��C��E�����Բ��BD�ཻ�ڵ�F����CD�ཻ�ڵ�G�����ABC�����ƽ�����ཻ�ڵ�H��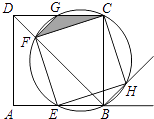
��1����֤���ı���EFCH�������Σ�
��2����BE=x����CFG�����Ϊy����y��x�ĺ�����ϵʽ������y�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺��һ���ı����д����������ߵ�ƽ���͵���һ���Խ��ߵ�ƽ�����������ı���Ϊ�����ı��Σ����������ڵı߳�Ϊ����ı��εĹ��ɱߣ�
��1��д������ѧ���������ı������ǹ����ı��ε�����ͼ�ε���������������������������������
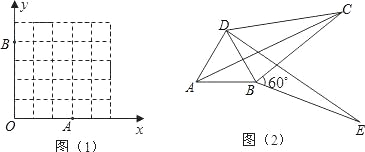
��2����ͼ1����֪��㣨С�����εĶ��㣩O��0��0����A��3��0����B��0��4��������ֱ��д�������Ը��Ϊ���㣬OA��OBΪ���ɱ����жԽ�����ȵĹ����ı���OAMB�Ķ���M�����꣮
��3����ͼ2������ABC�ƶ���B��˳ʱ�뷽����ת60�㣬�õ���DBE������AD��DC����DCB=30�㣮��֤��DC2+BC2=AC2�����ı���ABCD�ǹ����ı��Σ�
��4������ͼ2�С�ABC�ƶ���B��˳ʱ�뷽����תa�ȣ�0�㣼a��90�㣩���õ���DBE������AD��DC�����DCB=�������������㣬�ı���ABCD�ǹ����ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߶�AB��x���ϵ�A��B������ֱ�Ϊ����1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD����ƽ���ı���ABDC

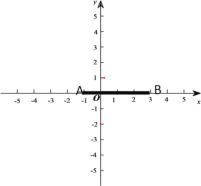
��1����ȫͼ�Σ�ֱ��д����C��D�����ꣻ
��2������y���ϴ��ڵ�M������MA��MB��ʹS��MAB=S�ı���ABDC�������M�����꣮
��3������P��ֱ��BD���˶�������PC��PO���뻭��ͼ�Σ�̽����CPO����DCP����BOP��������ϵ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��MON = 50����OE ƽ�֡�MON����A��B��C�ֱ�������OM��OE��ON�ϵĶ���(A��B��C�����O�غ�)������AC������OE�ڵ�D�����OAC = x�㣮
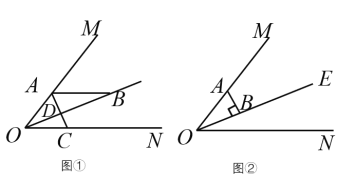
��1����ͼ�٣���AB//ON��
�����ABO �Ķ�����________��
�ڵ���BAD =��ABD ʱ��x=_______������BAD = ��BDA ʱ��x=________��
��2����ͼ�ڣ���AB��OE�����Ƿ����������xֵ��ʹ�� ��ABD ����һ��������һ���ǵ����������ڣ�ֱ��д��x��ֵ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015��ij��ҵ���ͳ�����������50Ԫ/�֡���������������20Ԫ/�ֵ��շѱ�����֧���ͳ��ͽ�������������7000Ԫ����2016��Ԫ�����շѱ��ϵ�Ϊ���ͳ�����������120Ԫ/�֣���������������40Ԫ/�֣�������ҵ2016�괦��������������������2015�����û�б仯����Ҫ��֧������������8600Ԫ��
��1������ҵ2015�괦���IJͳ������ͽ������������ٶ֣�
��2������ҵ�ƻ�2016�꽫�����������������������ٵ�200�֣��ҽ��������������������ͳ�������������3������2016�����ҵ������Ҫ֧�����������������ѹ�����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com