
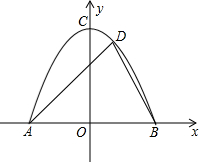
 某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-
某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,△ABC中,已知BE⊥AD,CF⊥AD,且BE=CF.
如图,△ABC中,已知BE⊥AD,CF⊥AD,且BE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知二次函数y=ax2+bx+3的图象与x轴交于点A(1,0)与B(3,0),交y轴于点C,其图象顶点为D.
已知二次函数y=ax2+bx+3的图象与x轴交于点A(1,0)与B(3,0),交y轴于点C,其图象顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2x-6 |
| x2-4x+4 |
| (x+3)(x-2) |
| 3-x |
| x2-y2 |
| xy |
| x |
| x-y |
| 4x2y |
| 4y2-x2 |
| 4y2 |
| x-2y |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 12 |
| 13 |
| 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用y(元)随时间x(天)的变化图象为折线OA-AB-BC,如图所示.
某汽车租赁公司对某款汽车的租赁方式按时段计费,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还.租赁费用y(元)随时间x(天)的变化图象为折线OA-AB-BC,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com