
分析 根据反比例函数y2=$\frac{{k}_{2}}{x}$的图象过点A(2,1)利用待定系数法即可求出k2,把B(n,2)代入反比例函数解析式即可求得B的坐标,然后利用待定系数法即可求得函数y1=k1x+b的解析式,即可求得k1,b.然后在同一坐标系画出函数y=-$\frac{2}{x}$和y=x+3的图象,根据图象求得即可.
解答 解:(1)因为函数y2=$\frac{{k}_{2}}{x}$的图象经过A(2,1),所以k2=2.
所以反比例函数的解析式为y=$\frac{2}{x}$.
因为B(n,2)在y=$\frac{2}{x}$上,所以n=1.
所以B的坐标是(1,2).
把A(2,1)、B(1,2)代入y1=k1x+b得:
$\left\{\begin{array}{l}{2{k}_{1}+b=1}\\{{k}_{1}+c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=-1}\\{b=3}\end{array}\right.$,
∵-$\frac{{k}_{2}}{x}$<-k1x+b化为:-$\frac{2}{x}$<x+3,
画出函数y=-$\frac{2}{x}$和y=x+3的图象如图: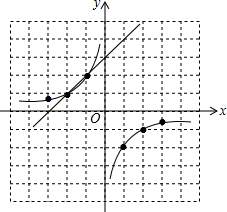
由图象可知等式-$\frac{{k}_{2}}{x}$<-k1x+b的解集x>0或-2<x<-1.
故答案为:x>0或-2<x<-1.
点评 此题主要考查了待定系数法求出反比例函数、一次函数解析式以及函数的图象,画出函数图象是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | -9 | B. | 9 | C. | 5 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
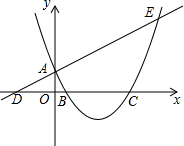 如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
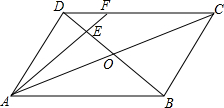 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△BAE=( )
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△BAE=( )| A. | 1:4 | B. | 1:3 | C. | 1:8 | D. | 1:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )| A. | 每月阅读数量的平均数是50 | B. | 众数是42 | ||
| C. | 中位数是58 | D. | 每月阅读数量超过40的有4个月 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
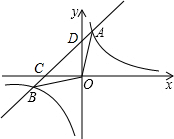 已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.
已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
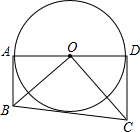 如图,⊙O的直径AD=8,AB、CD是⊙O的两条切线,AB=3,CD=$\frac{16}{3}$
如图,⊙O的直径AD=8,AB、CD是⊙O的两条切线,AB=3,CD=$\frac{16}{3}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com