
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,D为BC边上一点,CD=3,过A,C,D三点的⊙O与斜边AB交于点E,连结DE.
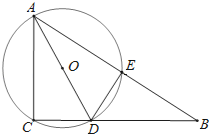
(1)求证:△BDE∽△BAC;
(2)求△ACD外接圆的直径的长;
(3)若AD平分∠CAB,求出BD的长.
【答案】(1)见解析;(2)3![]() ;(3)BD=5.
;(3)BD=5.
【解析】
试题分析:(1)由圆周角定理可证∠AED=90°,所以∠DEB=90°,再由公共角相等即可证明△BDE∽△BAC;
(2)由圆周角定理可证明AD是△ACD外接圆的直径,在直角三角形ACD中利用勾股定理可求出AD的长,问题得解;
(3)设BD=x,则BC=CD+x,由勾股定理可求出AB的长,由(1)可知△BDE∽△BAC,利用相似三角形的性质:对应边的比值相等可得到关于x的比例式,进而可求出x的值,BD的长得解.
解:(1)∵∠ACB=90°,
∴AD是圆的直径,
∴∠AED=90°,
∴∠DEB=90°,
又∵∠B=∠B,
∴△BDE∽△BAC;
(2)∵∠ACB=90°,
∴AD是圆的直径,
∵AC=6,CD=3,
∴AD=![]() =
=![]() =3
=3![]() ;
;
(3)∵AD平分∠CAB,AE⊥DE,AC⊥CD,
∴CD=DE=3,
设BD=x,则BC=CD+x=3+x,
在Rt△ACB中,AB=![]() =
=![]() ,
,
∵△BDE∽△BAC,
∴![]() ,
,
即![]() ,
,
∴4x2=62+(3+x)2,
解得:x=5或﹣3(舍),
∴BD=5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
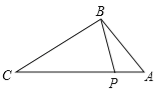
A. ∠ABP=∠C B. ∠APB=∠ABC C. ![]() =
=![]() D.
D. ![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“丰收1号“小麦的试验田是边长为am(a>1)的正方形去掉一个边长为1m的正方蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a﹣1)m的正方形,两块试验田的小麦都收获了500kg,试说明哪种小麦的单位面积产量高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC边上,且∠ADE=60°.
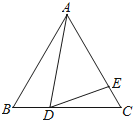
(1)求证:△ABD∽△DCE.
(2)若AB=9cm,BD=3cm,求EC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com