
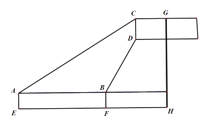
【题目】如图,小红在A处用测量仪测得某矩形广告牌顶端C的仰角为30°,然后前进10m到达B点,此时测得D处的仰角为60°,已知小红的身高AE=1.5m,广告牌CD的高度为2m,请你根据以上数据计算GH的长.
【答案】![]()
【解析】
延长CD分别交AB、EF于M、N.这样就形成了Rt△BDM和Rt△CAM. Rt△BDM中,假设BM=x,根据![]() =tan60°,能够得出DM、CM、AM的字母表达式,再根据Rt△CAM中,∠CAM=30° ,能够得出
=tan60°,能够得出DM、CM、AM的字母表达式,再根据Rt△CAM中,∠CAM=30° ,能够得出![]() =
=![]() ,从而得出
,从而得出![]() CM= AM,将上面所得AM,CM的字母表达式代入即可得x,从而得到DM的值,最后得出CN的值.
CM= AM,将上面所得AM,CM的字母表达式代入即可得x,从而得到DM的值,最后得出CN的值.
.解:延长CD分别交AB、EF于M、N.
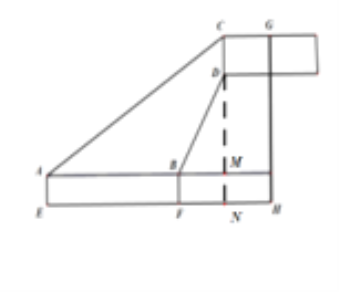
∴AB=10m、 AE=MN=1.5m、CD=2m、∠CAM=30° 、∠DBM=60°,
在Rt△BDM中,∠DBM=60°,设BM=x,
∴![]() =tan60°=
=tan60°=![]() .
.
∴DM=![]() x,CM=2+
x,CM=2+![]() AM=10+x,
AM=10+x,
在Rt△CAM中, ∠CAM=30° ,
则cot30°=![]() ,
,
∴![]() CM= AM,
CM= AM,
∴![]() ,
,
![]() ,
,
∴DM =5![]() -3,
-3,
∴CN=2+5![]() -3+1.5=(5
-3+1.5=(5![]() )m.
)m.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,A、B均为格点.
(I).![]() 的长等于_________;
的长等于_________;
(II).请用无刻度的直尺,在如图所示的网格中求作一点![]() ,使得以
,使得以![]() 为底边的等腰三角形
为底边的等腰三角形![]() 的面积等于
的面积等于![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明);_____________
的位置是如何找到的(不要求证明);_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据公开报道,2017年全国教育经费总投入为42557亿元,比上年增长9.43%,其中投入在各学段的经费占比(即所占比例)如图,根据图中提供的信息解答下列问题.
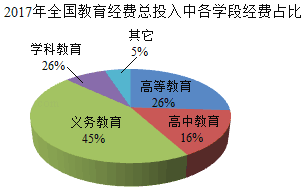
(1)在2017年全国教育经费总投入中,义务教育段的经费总投入应该是多少亿元?
(2)2016年全国教育经费总投入约为多少亿元?(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=58°,则∠ABC的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=58°,则∠ABC的度数为( )
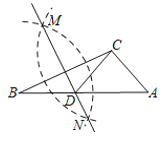
A. 29°B. 30°C. 31°D. 32°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金堂三溪镇被中国柑桔研究所誉为“中国脐橙第一乡”,2016年12月某公司到三溪镇以2.5元/千克购得脐橙12000千克,这些脐橙的销售期最多还有60天,60天后库存的脐橙不能再销售,需要当垃圾处理,处理费为0.1元/千克,经测算,脐橙的销售价格定为8元/千克时,每天可售出100千克;销售单价每降低0.5元,每天可多售出50千克.
(1).如果按8元/千克的价格销售,能否在60天内售完?这些脐橙按此价格销售,获得的利润是多少?
(2).如果按6元/千克的价格销售,这些脐橙获得的利润是多少?当这些脐橙销售价格定为x(![]() )元/千克时,可以使公司每天获得利润最大,每天的最大利润为多少?
)元/千克时,可以使公司每天获得利润最大,每天的最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
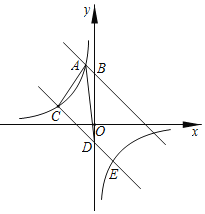
【题目】如图,在平面直角坐标系中,直线AB与y轴交于点![]() ,与反比例函数
,与反比例函数![]() 在第二象限内的图象相交于点
在第二象限内的图象相交于点![]() .
.
(1)求直线AB的解析式;
(2)将直线AB向下平移9个单位后与反比例函数的图象交于点C和点E,与y轴交于点D,求![]() 的面积;
的面积;
(3)设直线CD的解析式为![]() ,根据图象直接写出不等式
,根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某磨具厂共有六个生产车间,第一、二、三、四车间毎天生产相同数量的产品,第五、六车间每天生产的产品数量分別是第一车间每天生产的产品数量的![]() 和
和![]() .甲、乙两组检验员进驻该厂进行产品检验,在同时开始检验产品时,每个车间原有成品一样多,检验期间各车间继续生产.甲组用了6天时间将第一、二、三车间所有成品同时检验完;乙组先用2天将第四、五车间的所有成品同时检验完后,再用了4天检验完第六车间的所有成品(所有成品指原有的和检验期间生产的成品).如果每个检验员的检验速度一样,则甲、乙两组检验员的人数之比是________.
.甲、乙两组检验员进驻该厂进行产品检验,在同时开始检验产品时,每个车间原有成品一样多,检验期间各车间继续生产.甲组用了6天时间将第一、二、三车间所有成品同时检验完;乙组先用2天将第四、五车间的所有成品同时检验完后,再用了4天检验完第六车间的所有成品(所有成品指原有的和检验期间生产的成品).如果每个检验员的检验速度一样,则甲、乙两组检验员的人数之比是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
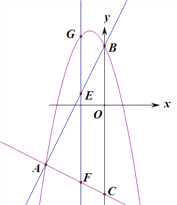
【题目】如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-![]() x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB、EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH、HF,当点E运动到什么位置时,以A、E、F、H为顶点的四边形是矩形?求出此时点E、H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求![]() AM+CM的最小值.
AM+CM的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com