
【题目】如图,在每个小正方形的边长为1的网格中,A、B均为格点.
(I).![]() 的长等于_________;
的长等于_________;
(II).请用无刻度的直尺,在如图所示的网格中求作一点![]() ,使得以
,使得以![]() 为底边的等腰三角形
为底边的等腰三角形![]() 的面积等于
的面积等于![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明);_____________
的位置是如何找到的(不要求证明);_____________

【答案】![]() 如图,取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.
如图,取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.
【解析】
(I)直接利用勾股定理即可得出答案;(II)如图,根据网格的特点取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.
(I)AB=![]() =
=![]() ,
,
(II)∵要作等腰三角形,P点须在AB的垂直平分线上,
∴取格点C,连接BC;取格点D,连接DC得点F;
根据网格的性质可知点G、F为AB、CD的中点,FG⊥AB,即,FG是AB的垂直平分线,
∵S△PAB=![]() ,AB=
,AB=![]() ,
,
∴△PAB底边AB上的高PG=![]() ,
,
∵FG=BC=AB=![]() ,
,
∴![]() ,
,
∵点G为小正方形的中点,
∴![]() ,
,
∴过格点E作AB的平行线,交FG于P,根据平行线分线段成比例定理可得点P即为所求.

故答案为:![]() ;如图,取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.
;如图,取格点C,连接BC;取格点D,连接DC得点F;点G是AB与网格的交点,连接FC;取格点H,E,连接HE,线段HE交FG于点P即为所求.


科目:初中数学 来源: 题型:
【题目】某村2016年的人均收入为20000元,2018年的人均收入为24200元
(1)求2016年到2018年该村人均收入的年平均增长率;
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年村该村的人均收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() ),其对称轴是
),其对称轴是![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() ,
,![]() 之间.有下列结论:①
之间.有下列结论:①![]() ;②
;②![]() ;③若此抛物线过
;③若此抛物线过![]() 和
和![]() 两点,则
两点,则![]() ,其中,正确结论的个数为( )
,其中,正确结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的一边AB在x轴上,∠ABC=90°,点C(4,8)在第一象限内,AC与y轴交于点E,抛物线y=![]() +bx+c经过A. B两点,与y轴交于点D(0,6).
+bx+c经过A. B两点,与y轴交于点D(0,6).
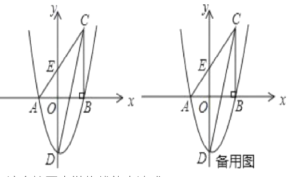
(1)请直接写出抛物线的表达式;
(2)求ED的长;
(3)点P是x轴下方抛物线上一动点,设点P的横坐标为m,△PAC的面积为S,试求出S与m的函数关系式;
(4)若点M是x轴上一点(不与点A重合),抛物线上是否存在点N,使∠CAN=∠MAN.若存在,请直接写出点N的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).
经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).
(I).求抛物线的解析式及它的对称轴;
(Ⅱ)点![]() 在线段OB上,点Q在线段BC上,若
在线段OB上,点Q在线段BC上,若![]() ,且
,且![]() ,求n的值;
,求n的值;
(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三形?若存在,求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
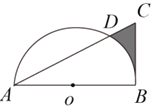
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红在A处用测量仪测得某矩形广告牌顶端C的仰角为30°,然后前进10m到达B点,此时测得D处的仰角为60°,已知小红的身高AE=1.5m,广告牌CD的高度为2m,请你根据以上数据计算GH的长.
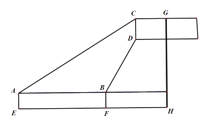
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com