
已知关于x的方程x2+px﹣15=0的两根之差的绝对值是8,则P的值是( )
A.±2 B.2 C.﹣2 D.±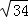
A【考点】根与系数的关系.
【分析】根据根与系数的关系x1•x2=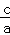 、x1+x2=﹣
、x1+x2=﹣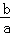 得出x1+x2=﹣p,x1•x2=﹣15,再根据(a﹣b)2=(a+b)2﹣4ab代入计算即可.
得出x1+x2=﹣p,x1•x2=﹣15,再根据(a﹣b)2=(a+b)2﹣4ab代入计算即可.
【解答】解:∵方程x2+px﹣15=0的二次项系数a=1,一次项系数b=p,常数项c=﹣15,
∴x1+x2=﹣p,x1•x2=﹣15,
∵方程x2+px﹣15=0的两根之差的绝对值是8,
∴|x1﹣x2|=8,
∴(x1﹣x2)2=64,
∴(x1+x2)2﹣4x1•x2=64,
∴(﹣p)2﹣4×(﹣15)=64,即p2+60=64,
解得p=±2.
故选A.
【点评】本题主要考查了根与系数的关系.解答此题时,要灵活运用完全平方公式的变形,在该题中就利用了(a﹣b)2=(a+b)2﹣4ab.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
下列命 题中假命题是( )
题中假命题是( )
A.一个三角形中至少有一个角不大于60度
B.有一个外角是锐角的三角形是钝角三角形
C.锐角三角形中,两个角的和小于直角
D.直角三角形中,有一个外角等于和它的相邻的内角
查看答案和解析>>
科目:初中数学 来源: 题型:
对于任意实数k,关于x的方程x2﹣2(k+1)x﹣k2+2k﹣1=0的根的情况为( )
A.有两个相等的实数根 B.没有实数根
C.有两个不相等的实数根 D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,二次函数y=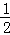 x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP=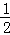 S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
在数学学习过程中,我们常常会有“似曾相识”的感觉,如果我们把这些类似进行比较、加以联想的话,可能出现许多意想不到的结果和方法,这种把类似进行比较、联想,从而解决问题的方法就是类比法.类比法是一种寻求解题思路,猜测问题答案或结论的发现方法.
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
【尝试探索】
①经过三角形顶点的面积等分线有 ________条;
②平行四边形有 ________条面积等分线.
【类比探究】
如图所示,在矩形中剪去一个小正方形,请画出这个图形的一条面积等分线;
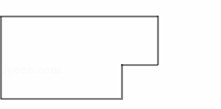
【类比拓展】
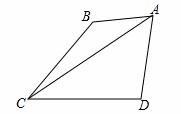 如图,四边形ABCD中,AB与CD不平行,AB≠CD,且S△ABC<S△ACD,过点A画出四边形ABCD的面积等分线,并描述方法.
如图,四边形ABCD中,AB与CD不平行,AB≠CD,且S△ABC<S△ACD,过点A画出四边形ABCD的面积等分线,并描述方法.
解:
【灵活运用】
请您尝试画出一种图形,并画出它的一条面积等分线。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com