
【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形B,C,E在同一条直线上,连结DC. 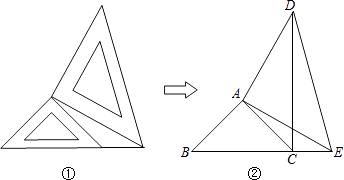
(1)请找出图②中的全等三角形,并给予说明(注意:结论中不得含有未标识的字母);
(2)请判断DC与BE的位置关系,并证明;
(3)若CE=2,BC=4,求△DCE的面积.
【答案】
(1)解:△ABE≌△ACD,
∵△ABC和△ADE是等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,
∴∠BAC+∠EAC=∠DAE+∠EAC,
∴∠BAE=∠CAD,
在△ABE和△ACD中,
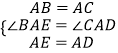
∴△ABE≌△ACD(SAS)
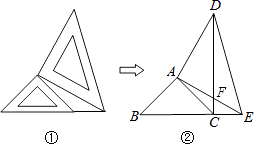
(2)解:∵△ABE≌△ACD,
∴∠AEB=∠ADC.
∵∠ADC+∠AFD=90°,
∴∠AEB+∠AFD=90°.
∵∠AFD=∠CFE,
∴∠AEB+∠CFE=90°,
∴∠FCE=90°,
∴DC⊥BE
(3)解:∵CE=2,BC=4,
∴BE=6,
∵△ABE≌△ACD,
∴CD=BE=6,
∴△DCE的面积= ![]() CECD=
CECD= ![]() ×2×6=6
×2×6=6
【解析】(1)根据等腰直角三角形的性质可以得出△ABE≌△ACD;(2)由△ABE≌△ACD可以得出∠AEB=∠ADC,进而得出∠AEC=90°,就可以得出结论;(3)根据三角形的面积公式即可得到结论.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.

(1)求这条抛物线对应的函数解析式;
(2)求直线AB对应的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2 + 4x – 5 = 0,此方程可变形为( )
A. (x + 2)2 = 9B. (x - 2)2 = 9
C. (x + 2)2 = 1D. (x - 2)2 =1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A. <span style="color: rgb(169, 68, 66); font-size: 12px; line-height: 17.1429px; background-color: rgb(245, 245, 245);">经过直线外一点,有且只有一条直线与已知直线垂直</span>
B. 平分弦的直径垂直于弦。
C. 对角线互相平分且垂直的四边形是菱形 。
D. 反比例函数![]() ,当k<0时,y随x的增大而增大。
,当k<0时,y随x的增大而增大。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某土建工程共需动用15台挖运机械,每台机械每分钟能挖土3m3或者运土2m3 . 为了使挖土和运土工作同时结束,安排了x台机械运土,这里x应满足的方程是( )
A.2x=3(15﹣x)
B.3x﹣2x=15
C.15﹣2x=3x
D.3x=2(15﹣x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知射线AB∥射线CD,P为一动点,AE平分∠PAB,CE平分∠PCD,且AE与CE相交于点E.
(1)在图1中,当点P运动到线段AC上时,∠APC=180°. ①直接写出∠AEC的度数;②求证:∠AEC=∠EAB+∠ECD;
(2)当点P运动到图2的位置时,猜想∠AEC与∠APC之间的关系,并加以说明;
(3)当点P运动到图3的位置时,(2)中的结论是否还成立?若成立,请说明理由;若不成立,请写出∠AEC与∠APC之间的关系,并加以证明. 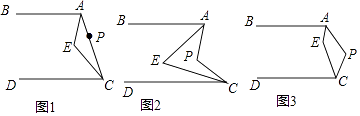
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com