
【题目】如图一,∠ACB=90°,点D在AC上,DE⊥AB垂足为E,交BC的延长线于F,DE=EB,EG=EB,
(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图二,找出图中与AB相等的线段,并证明.
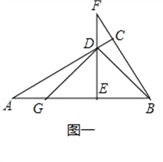

【答案】(1)证明见解析; (2)AB=DM,证明见解析.
【解析】分析:(1)根据已知条件得到DE=EB=EB,∠EGD=∠EGD=∠EDB=∠EBD=45°,进而证得∠AGD=∠FDB=135°,根据三角形内角和证得∠A=∠F,由三角形外角定理证得∠ADG=∠FBD,根据三角形的判定证得△ADG≌△FDB,由全等三角形的判定即可证得结论;
(2)根据已知条件得到△AED≌△FEB,由全等三角形的性质得到AE=EM,即可得到结论.
本题解析:(1)∵DE=EB,EG=EB,DE⊥AB,
∴DE=EB=EG,
∴∠EGD=∠EDG=∠EDB=∠EBD=45°,
∴∠AGD=∠FDB=135°,
∵∠ACB=90°,∠AED=90°,∠ADE=∠FDC,
∴∠A=∠F,
∴∠ADG=∠FBD,
在△ADG和△FDB中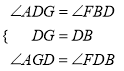
∴△ADG≌△FDB,
∴AG=DF;
(2)∵DE=EB,EG=EB,
∴DE=EB=EG,∵DE⊥AB,
在△AED和△FEB中, 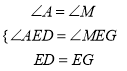
∴△AED≌△MEB,
∴AE=EM,
∴AE+EB=EM+DE,
即AB=DM.


科目:初中数学 来源: 题型:
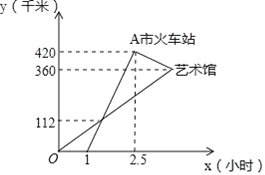
【题目】高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离开N市的距离y与乘车时间x的函数关系式;
(3)若甲要提前30分钟到达艺术馆,那么私家车的速度必须达到多少千米/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
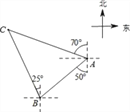
A. 10![]() 海里 B. 10
海里 B. 10![]() 海里 C. 10
海里 C. 10![]() 海里 D. 20
海里 D. 20![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
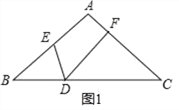
【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,求证:DECD=DFBE
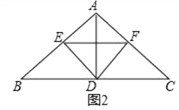
(2)D为BC中点如图2,连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=40°,AB的垂直平分线MN交AC于点D,∠DBC=30°,若AB=m,BC=n,则△DBC的周长为( )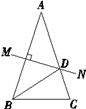
A.m+n
B.2m+n
C.m+2n
D.2m -n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式中,成立的是( )
A. (a+b)2=a2+b2B. (a-b)2=a2-b2
C. (-a+b)(a-b)=a2-b2D. (a-b)2=a2-2ab+b2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com