
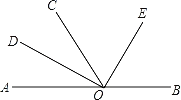
【题目】如图,O为直线AB上一点,∠AOC=58°,OD平分∠AOC,∠DOE=90°.
(1)求出∠BOD的度数;
(2)请通过计算说明:OE是否平分∠BOC.
【答案】(1)∠BOD=151°;(2)见解析;
【解析】
(1)根据∠AOC=58°,OD平分∠AOC求出∠AOD的度数,再根据邻补角的定义即可得出∠BOD的度数;
(2)根据∠AOC=58°求出∠BOC的度数,再由OD平分∠AOC求出∠DOC的度数,根据∠DOC与∠COE互余,即可得出∠COE的度数,进而可得出结论.
(1)∵∠AOC=58°,OD平分∠AOC,
∴∠AOD=![]() ∠AOC =29°,
∠AOC =29°,
∴∠BOD=180°﹣∠AOD =180°﹣29°=151°;
(2)OE是∠BOC的平分线.理由如下:
∵∠AOC=58°,
∴∠BOC=122°.
∵OD平分∠AOC,
∴∠DOC=![]() ×58°=29°.
×58°=29°.
∵∠DOE=90°,
∴∠COE=90°﹣29°=61°,
∴∠COE=![]() ∠BOC,即OE是∠BOC的平分线.
∠BOC,即OE是∠BOC的平分线.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】已知A. B两地果园分别有苹果30吨和40吨,C. D两地的农贸市场分别需求苹果20吨和50吨。已知从A. B两地到C. D两地的运价如表:
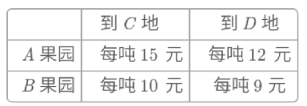
(1)填空:若从A果园运到C地的苹果为10吨,则从A果园运到D地的苹果为___吨,从B果园运到C地的苹果为___吨,从B果园运到D地的苹果为___吨,总运输费为___元;
(2)如果总运输费为750元时,那么从A果园运到C地的苹果为多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】右图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A、B、C、D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )
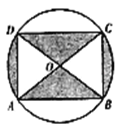
A. 5πcm2 B. 10πcm2 C. 15πcm2 D. 20πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
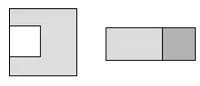
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2
D.a2-ab=a(a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,![]() 是函数
是函数![]() 的图像上一点,
的图像上一点,![]() 是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
(1)求a的值;
(2)如图②,当![]() 时,求点P的坐标;
时,求点P的坐标;
(3)若点P也在函数![]() 的图像上,求b的值;
的图像上,求b的值;
(4)设正方形ABPQ的中心为M,点N是函数![]() 的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
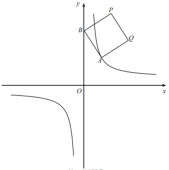
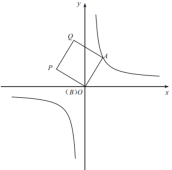

图① 图② 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个正方形ABCD,点P是边BC上一点.将![]() 绕点A逆时针方向旋转90°得到
绕点A逆时针方向旋转90°得到![]() (点B,P的对应点分别是
(点B,P的对应点分别是![]() )
)
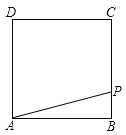
(1)画出旋转后所得到的![]() ;
;
(2)联结![]() ,设
,设![]() ,
,![]() ,试用
,试用![]() 表示
表示![]() 的面积;
的面积;
(3)若![]() 的面积为18,
的面积为18,![]() 的面积为5,试求PC的长.
的面积为5,试求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为![]() ,连接CF,则CF= .
,连接CF,则CF= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com