
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
x﹣2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( ) 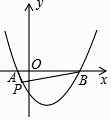
A.﹣1<m<0
B.﹣1<m<0或3<m<4
C.0<m<3或m>4
D.m<﹣1或0<m<3
【答案】B
【解析】解:令y=0得: ![]() x2﹣
x2﹣ ![]() x﹣2=0, 解得:x=﹣1或x=4,
x﹣2=0, 解得:x=﹣1或x=4,
则点A(﹣1,0)、B(4,0),
以AB为直径作圆M,与y轴交于点P.则抛物线在圆内的部分如图所示,能使∠APB为钝角,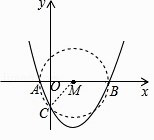
∴M( ![]() ,0),⊙M的半径=
,0),⊙M的半径= ![]() .
.
在Rt△OMP中,∴OP= ![]() =2.
=2.
∴P(0,﹣2),
由抛物线的对称性可知,P′(3,﹣2),
∴当﹣1<m<0或3<m<4时,∠APB为钝角,
故选:B.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F. 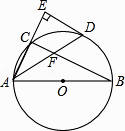
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 380元/辆 |
| 20人/辆 | 280元/辆 |
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AB//DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C﹣D﹣A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l//AD,与线段CD的交点为E,与折线A﹣C﹣B的交点为Q.点M运动的时间为t(秒).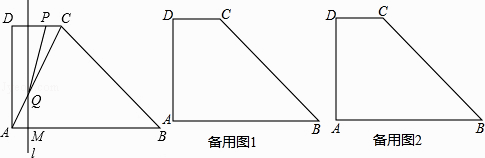
(1)当t=0.5时,求线段QM的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究 ![]() 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意设未知数,并列出方程(不必求解).
(1)有两个工程队,甲队人数30名,乙队人数10名,问怎样调整两队的人数,才能使甲队的人数是乙队人数的7倍.
(2)有一个班的同学准备去划船,租了若干条船,他们计算了一下,如果比原计划多租1条船,那么正好每条船坐6人;如果比原计划少租1条船,那么正好每条船坐9人.问这个班共有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:善于思考的小明在解方程组![]() 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:
解:将方程②8x+20y+2y=10,变形为 2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则 y=﹣1;把 y=﹣1 代入①得,x=4,所以方程组的解为:![]() 请你解决以下问题:
请你解决以下问题:
(1)试用小明的“整体代换”的方法解方程组![]()
(2)已知 x、y、z,满足![]() 试求 z 的值.
试求 z 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC的边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则y与x函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com