
【题目】如图,![]() 的中线BD,CE交于点O,F,G分别是BO,CO的中点.
的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)求证:四边形DEFG是平行四边形;
(2)若AB=AC,则四边形DEFG是 (填写特殊的平行四边形);
(3)当四边形DEFG为边长为2的正方形时,![]() 的周长为 .
的周长为 .

【答案】(1)证明见解析;(2)矩形;(3)![]() .
.
【解析】
(1)先根据三角形的中位线定理可得![]() ,再根据平行线的性质可得
,再根据平行线的性质可得![]() ,然后根据平行四边形的判定即可得证;
,然后根据平行四边形的判定即可得证;
(2)先根据等腰三角形的判定与性质可得![]() ,再根据三角形重心的性质可得
,再根据三角形重心的性质可得![]() ,从而可得
,从而可得![]() ,然后根据矩形的判定即可得;
,然后根据矩形的判定即可得;
(3)先根据正方形的性质可得![]() ,再根据中位线定理可得BC的长,然后根据三角形重心的性质可得OB的长,从而利用勾股定理可得BD、CD的长,最后根据线段中点的定义可得AB、AC的长,由此即可得出答案.
,再根据中位线定理可得BC的长,然后根据三角形重心的性质可得OB的长,从而利用勾股定理可得BD、CD的长,最后根据线段中点的定义可得AB、AC的长,由此即可得出答案.
(1)![]() BD、CE是
BD、CE是![]() 的中线
的中线
![]() 是
是![]() 的中位线
的中位线
![]()
同理可得:![]()
![]()
![]() 四边形DEFG是平行四边形;
四边形DEFG是平行四边形;
(2)![]()
![]() 是等腰三角形
是等腰三角形
![]() BD、CE是等腰
BD、CE是等腰![]() 两腰上的中线
两腰上的中线
![]() ,交点O为
,交点O为![]() 的重心
的重心
![]()
![]()
![]() 四边形DEFG是平行四边形
四边形DEFG是平行四边形
![]()
![]()
![]() 平行四边形DEFG是矩形
平行四边形DEFG是矩形
故答案为:矩形;
(3)![]() 四边形DEFG为边长为2的正方形
四边形DEFG为边长为2的正方形
![]()
![]()
![]() ,
,![]()
![]()
由(2)知,![]()
![]()
![]()
在![]() 中,
中,![]()
同理可得:![]()
![]() BD、CE是
BD、CE是![]() 的中线,即点D、E分别是AC、AB的中点
的中线,即点D、E分别是AC、AB的中点
![]()
由(1)知,![]()
![]()
则![]() 的周长为
的周长为![]()
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为________.
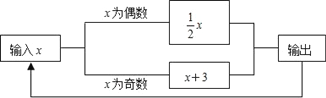
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为![]() m.
m.
(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是![]() ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
(参考数据:sin22°≈![]() ,tan22°≈
,tan22°≈![]() ,sin31°≈
,sin31°≈![]() ,tan31°≈
,tan31°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=a![]() +bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )

A. abc<0 B. 2a+b<0 C. a-b+c<0 D. 4ac-b2<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:小聪在一张长条形的纸面上画了一条数轴(如图所示),
![]()
操作一:(1)折叠纸面,使1表示的点与1的点重合,则3的点与_ __表示的点重合;
操作二:(2)折叠纸面,使2表示的点与6表示的点重合,请你回答以下问题:
① 5表示的点与数___表示的点重合;
② 若数轴上A、B两点之间距离为20,其中A在B的左侧,且A、B两点经折叠后重合,求A、B两点表示的数各是多少
③ 已知在数轴上点M表示的数是m,点M到第②题中的A、B两点的距离之和为30,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2﹣
x2﹣![]() x+3与x轴交于A,B两点,与y轴交于点C,点M的坐标为(2
x+3与x轴交于A,B两点,与y轴交于点C,点M的坐标为(2![]() , 1).以M为圆心,2为半径作⊙M.则下列说法正确的是________(填序号).
, 1).以M为圆心,2为半径作⊙M.则下列说法正确的是________(填序号).
①tan∠OAC=![]() ;
;
②直线AC是⊙M的切线;
③⊙M过抛物线的顶点;
④点C到⊙M的最远距离为6;
⑤连接MC,MA,则△AOC与△AMC关于直线AC对称.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填在相应的集合里:
-2.4,3,![]() ,
,![]() ,0.333…,-(2.28),3.14,
,0.333…,-(2.28),3.14,![]() ,1.010010001…(相邻两个1之间0的个数增加1),
,1.010010001…(相邻两个1之间0的个数增加1),![]() .
.
(1)正有理数集合{ ……}
(2)整数集合{ ……}
(3)负分数集合{ ……}
(4)无理数集合{ ……}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com