
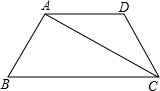
 解:∵AD∥BC,
解:∵AD∥BC,

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
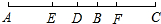 如图,已知线段AB和CD的公共部分BD=
如图,已知线段AB和CD的公共部分BD=| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
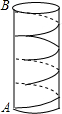 为了庆祝“元旦”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为1m,高为3m.如果要求彩带从柱子底端的A处绕柱子1圈后到达柱子顶端的B处(线段AB与地面垂直),那么彩带的长度最短为
为了庆祝“元旦”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为1m,高为3m.如果要求彩带从柱子底端的A处绕柱子1圈后到达柱子顶端的B处(线段AB与地面垂直),那么彩带的长度最短为查看答案和解析>>
科目:初中数学 来源: 题型:
A、1,1,
| ||
B、1,1,
| ||
C、1,2,
| ||
| D、1,2,3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com