
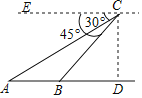
【题目】如图,在直升机的镜头下,观测牡丹园A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为200米,点A、B、D在同一条直线上,则A、B两点间的距离为___米.(结果保留根号)
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
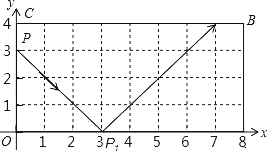
【题目】如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2的坐标是_____,点P2017的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
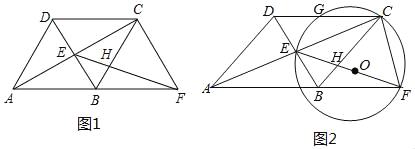
【题目】已知四边形ABCD是边长为10的菱形,对角线AC、BD相交于点E,过点C作CF∥DB交AB延长线于点F,联结EF交BC于点H.
(1)如图1,当EF⊥BC时,求AE的长;
(2)如图2,以EF为直径作⊙O,⊙O经过点C交边CD于点G(点C、G不重合),设AE的长为x,EH的长为y;
①求y关于x的函数关系式,并写出定义域;
②联结EG,当△DEG是以DG为腰的等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
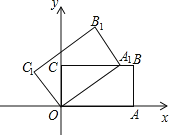
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点 A(2,m),B(2,m-5)在平面直角坐标系中,点O为坐标原点.若△ABO是直角三角形,则m的值不可能是( )
A.4B.2C.1D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
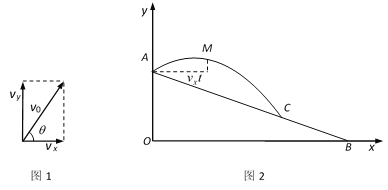
【题目】如图1,已知水龙头喷水的初始速度v0可以分解为横向初始速度vx和纵向初始速度vy,θ是水龙头的仰角,且![]() .图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为
.图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为![]() .离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为
.离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为![]() ;M与A的水平距离为
;M与A的水平距离为![]() 米.已知该水流的初始速度
米.已知该水流的初始速度![]() 为15米/秒,水龙头的仰角θ为
为15米/秒,水龙头的仰角θ为![]() .
.
(1)求水流的横向初始速度vx和纵向初始速度vy;
(2)用含t的代数式表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围);
(3)水流在山坡上的落点C离喷射点A的水平距离是多少米?若要使水流恰好喷射到坡脚B处的小树,在相同仰角下,则需要把喷射点A沿坡面AB方向移动多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM;④AM=![]() MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )
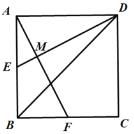
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
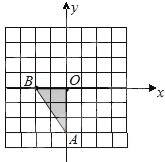
【题目】如图,在平面直角坐标系中,已知△AOB,A(0,﹣3),B(﹣2,0).将△OAB先绕点B 逆时针旋转90°得到△BO1A1,再把所得三角形向上平移2个单位得到△B1A2O2;
(1)在图中画出上述变换的图形,并涂黑;
(2)求△OAB在上述变换过程所扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com