
【题目】如图,已知△ABC中,AC=BC=5,AB=5![]() ,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.
,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.

 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() :y=2x+1与直线
:y=2x+1与直线 ![]() :y=mx+4相交于点P(1,b)
:y=mx+4相交于点P(1,b)
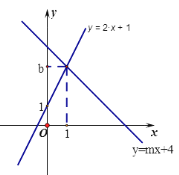
(1)求b,m的值
(2)垂直于x轴的直线 x=a与直线 ![]() ,
,![]() 分别相交于C,D,若线段CD长为2,求a的值
分别相交于C,D,若线段CD长为2,求a的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一位旅行者在早晨8时从城市出发到郊外所走的路程![]() 单位:千米
单位:千米![]() 与时间
与时间![]() 单位:时
单位:时![]() 的变量关系的图象.根据图象回答问题:
的变量关系的图象.根据图象回答问题:
![]() 在这个变化过程中,自变量是______ ,因变量是______ .
在这个变化过程中,自变量是______ ,因变量是______ .
![]() 时所走的路程是多少?他休息了多长时间?
时所走的路程是多少?他休息了多长时间?
![]() 他从休息后直至到达目的地这段时间的平均速度是多少?
他从休息后直至到达目的地这段时间的平均速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
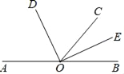
如图,已知点A,O,B在同一条直线上,OE平分∠BOC,∠DOE=90°
求证:OD是∠AOC的平分线;
证明:如图,因为OE是∠BOC的平分线,
所以∠BOE=∠COE.( )
因为∠DOE=90°
所以∠DOC+∠ =90°
且∠DOA+∠BOE=180°﹣∠DOE= °.
所以∠DOC+∠ =∠DOA+∠BOE.
所以∠ =∠ .
所以OD是∠AOC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
A.r≥1
B.1≤r≤ ![]()
C.1≤r≤ ![]()
D.1≤r≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:DC=BE;
(2)连接BF,若BF⊥AE,求证:△ADF≌△ECF.

查看答案和解析>>
科目:初中数学 来源: 题型:
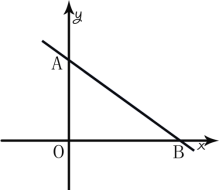
【题目】如图,直线MN与x轴、y轴分别相交于B、A两点,OA,OB的长满足式子![]()
(1)求A,B两点的坐标;
(2)若点O到AB的距离为![]() ,求线段AB的长;
,求线段AB的长;
(3)在(2)的条件下,x轴上是否存在点P,使ΔABP使以AB为腰的等腰三角形,若存在请直接写出满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线C1:y=a(x+1)2﹣4的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求点C的坐标及a 的值;
(2)如图②,抛物线C2与C1关于x轴对称,将抛物线C2向右平移4个单位,得到抛物线C3 . C3与x轴交于点B、E,点P是直线CE上方抛物线C3上的一个动点,过点P作y轴的平行线,交CE于点F.
①求线段PF长的最大值;
②若PE=EF,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习整式乘法时,老师拿出三种型号的卡片,如图1:A型卡片是边长为a的正方形,B型卡片是边长为b的正方形,C型卡片是长和宽分别为a,b的长方形。
(1)选取1张A型卡片,2张C型卡片,1张B型卡片,在纸上按照图2的方式拼成一个长为(a+b)的大正方形,通过不同方式表示大正方形的面积,可得到乘法公式:______________



(2)若用图1中的8块C型长方形卡片可以拼成如图3所示的长方形,它的宽为20cm,请你求出每块长方形的面积
(3)选取1张A型卡片,3张C型卡片按图4的方式不重叠地放在长方形DEFG框架内,已知GF的长度固定不变,DG的长度可以变化,图中两阴影部分(长方形)的面积分别表示为S1,S2,若S=S2-S1,则当a与b满足_________时,S为定值,且定值为___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com