
ЁОЬтФПЁПбЇЯАећЪНГЫЗЈЪБЃЌРЯЪІФУГіШ§жжаЭКХЕФПЈЦЌЃЌШчЭМ1ЃКAаЭПЈЦЌЪЧБпГЄЮЊaЕФе§ЗНаЮЃЌBаЭПЈЦЌЪЧБпГЄЮЊbЕФе§ЗНаЮЃЌCаЭПЈЦЌЪЧГЄКЭПэЗжБ№ЮЊaЃЌbЕФГЄЗНаЮЁЃ
ЃЈ1ЃЉбЁШЁ1еХAаЭПЈЦЌЃЌ2еХCаЭПЈЦЌЃЌ1еХBаЭПЈЦЌЃЌдкжНЩЯАДееЭМ2ЕФЗНЪНЦДГЩвЛИіГЄЮЊЃЈa+bЃЉЕФДѓе§ЗНаЮЃЌЭЈЙ§ВЛЭЌЗНЪНБэЪОДѓе§ЗНаЮЕФУцЛ§ЃЌПЩЕУЕНГЫЗЈЙЋЪНЃК______________



ЃЈ2ЃЉШєгУЭМ1жаЕФ8ПщCаЭГЄЗНаЮПЈЦЌПЩвдЦДГЩШчЭМ3ЫљЪОЕФГЄЗНаЮЃЌЫќЕФПэЮЊ20cmЃЌЧыФуЧѓГіУППщГЄЗНаЮЕФУцЛ§
ЃЈ3ЃЉбЁШЁ1еХAаЭПЈЦЌЃЌ3еХCаЭПЈЦЌАДЭМ4ЕФЗНЪНВЛжиЕўЕиЗХдкГЄЗНаЮDEFGПђМмФкЃЌвбжЊGFЕФГЄЖШЙЬЖЈВЛБфЃЌDGЕФГЄЖШПЩвдБфЛЏЃЌЭМжаСНвѕгАВПЗжЃЈГЄЗНаЮЃЉЕФУцЛ§ЗжБ№БэЪОЮЊS1ЃЌS2ЃЌШєS=S2-S1ЃЌдђЕБaгыbТњзу_________ЪБЃЌSЮЊЖЈжЕЃЌЧвЖЈжЕЮЊ___________.

ЁОД№АИЁПЃЈ1ЃЉa2+2ab+b2=ЃЈa+bЃЉ2ЃЛЃЈ2ЃЉ75 cm2ЃЛЃЈ3ЃЉa=2bЃЌa2-ab.
ЁОНтЮіЁП
ЃЈ1ЃЉНсКЯЭМаЮЃЌжБНггЩЕШЛ§ЗЈПЩЕУЭъШЋЦНЗНКЭЙЋЪНЃЛ
ЃЈ2ЃЉНсКЯЭМаЮЃЌНЈСЂЙигкaЃЌbЕФЖўдЊвЛДЮЗНГЬзщЃЌНтЗНГЬзщМДПЩЃЛ
ЃЈ3ЃЉЩшDGГЄЮЊxЃЌНсКЯЭМаЮЃЌгУКЌxЕФЪНзгЗжБ№БэЪОГіS1ЃЌS2ЃЌМЬЖјЕУЕНSЕФБэДяЪНЃЌИљОнSЮЊЖЈжЕЃЌгыxЮоЙиЃЌДгЖјЕУЕНaЃЌbЕФЙиЯЕЪНМАЖЈжЕЃЎ
НтЃКЃЈ1ЃЉAаЭПЈЦЌЕФУцЛ§ЮЊa2ЃЌBаЭПЈЦЌЕФУцЛ§ЮЊb2ЃЌCаЭПЈЦЌЕФУцЛ§ЮЊabЃЌ
ЬтжавбОбЁдё1еХAаЭПЈЦЌЃЌ2еХCаЭПЈЦЌЃЌвЛеХBаЭПЈЦЌЃЌУцЛ§жЎКЭЮЊa2+2ab+b2ЃЌгЩЭМПЩжЊЃЌвВе§КУЦДГЩСЫвЛИіБпГЄЮЊЃЈa+bЃЉЕФе§ЗНаЮЃЌгЩДЫПЩвдЕУЕНвЛИіЭъШЋЦНЗНЙЋЪНЃЌЙЪД№АИЮЊЃКa2+2ab+b2=ЃЈa+bЃЉ2ЃЛ
ЃЈ2ЃЉгЩЭМПЩЕУЙигкaЃЌbЕФЖўдЊвЛДЮЗНГЬ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
S=ab=5ЁС15=75 (cm2)
ЙЪУПИіCаЭГЄЗНаЮЕФУцЛ§ЮЊ75 cm2
ЃЈ3ЃЉЩшDGГЄЮЊxЃЌгЩЭМПЩжЊ
S1=a[x-ЃЈa+bЃЉ]=ax-a2-ab
S2=2bЃЈx-aЃЉ=2bx-2ab
S=S2-S1= 2bx-2ab-( ax-a2-ab)=(2b-a)x+a2-ab
гЩЬтвтЕУЃЌШєSЮЊЖЈжЕЃЌдђSНЋВЛЫцxЕФБфЛЏЖјБфЛЏЃЌ
ПЩжЊЕБ2b-a=0ЪБЃЌМДa=2bЪБЃЌS= a2-abЮЊЖЈжЕ
ЙЪД№АИЮЊЃКa=2bЃЌa2-ab.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌACЃНBCЃН5ЃЌABЃН5![]() ЃЌШ§НЧаЮЖЅЕудкЯрЛЅЦНааЕФШ§ЬѕжБЯпL1ЃЌL2ЃЌL3ЩЯЃЌЧвL2ЃЌL3жЎМфЕФОрРыЮЊ3ЃЌдђL1ЃЌL3жЎМфЕФОрРыЪЧ_____ЃЎ
ЃЌШ§НЧаЮЖЅЕудкЯрЛЅЦНааЕФШ§ЬѕжБЯпL1ЃЌL2ЃЌL3ЩЯЃЌЧвL2ЃЌL3жЎМфЕФОрРыЮЊ3ЃЌдђL1ЃЌL3жЎМфЕФОрРыЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуCЮЊСНЬѕЯрЛЅЦНааЕФжБЯпABЃЌEDжЎМфвЛЕуЃЌ![]() КЭ
КЭ![]() ЕФНЧЦНЗжЯпЯрНЛгкFЃЌШєЁЯBCD=
ЕФНЧЦНЗжЯпЯрНЛгкFЃЌШєЁЯBCD=![]() ЁЯBFD+10ЁуЃЌдђ
ЁЯBFD+10ЁуЃЌдђ![]() ЕФЖШЪ§ЮЊ__________ЃЎ
ЕФЖШЪ§ЮЊ__________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮАВШЋжЊЪЖВтбщжаЃЌбЇЩњЕУЗжОљЮЊећЪ§ЃЌТњЗж10ЗжЃЌетДЮВтбщжаМзЁЂввСНзщбЇЩњШЫЪ§ЖМЮЊ6ШЫЃЌГЩМЈШчЯТЃЈЕЅЮЛЃКЗжЃЉЃК
МзЃК7ЃЌ9ЃЌ10ЃЌ8ЃЌ5ЃЌ9ЃЛ
ввЃК9ЃЌ6ЃЌ8ЃЌ10ЃЌ7ЃЌ8
ЃЈ1ЃЉЧыВЙГфЭъећЯТУцЕФГЩМЈЭГМЦЗжЮіБэЃК
ЦНОљЗж | ЗНВю | жкЪ§ | жаЮЛЪ§ | |
Мззщ | 8 | 9 | ||
ввзщ |
| 8 | 8 |
ЃЈ2ЃЉМззщбЇЩњЫЕЫћУЧЕФжкЪ§ИпгкввзщЃЌЫљвдЫћУЧЕФГЩМЈКУгкввзщЃЌЕЋввзщбЇЩњВЛЭЌвтМззщбЇЩњЕФЫЕЗЈЃЌШЯЮЊЫћУЧзщЕФГЩМЈвЊКУгкМззщЃЌЧыФуИјГівЛЬѕжЇГжввзщбЇЩњЙлЕуЕФРэгЩЃЎ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
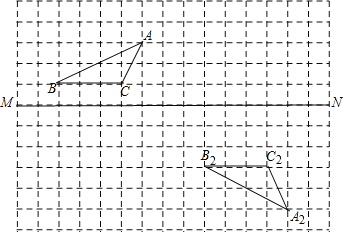
ЁОЬтФПЁПдкБпГЄЮЊ1ЕФе§ЗНаЮЭјИёжа
![]() зїГі
зїГі![]() ЙигкжБЯпMNЖдГЦЕФ
ЙигкжБЯпMNЖдГЦЕФ![]() ЃЛ
ЃЛ
![]() Шє
Шє![]() ОЙ§ЭМаЮЦНвЦЕУЕН
ОЙ§ЭМаЮЦНвЦЕУЕН![]() ЃЌЕБЕуAЕФзјБъЪЧ
ЃЌЕБЕуAЕФзјБъЪЧ![]() ЪБЃЌЧыНЈСЂЪЪЕБЕФжБНЧзјБъЯЕЃЌЗжБ№аДГіЕу
ЪБЃЌЧыНЈСЂЪЪЕБЕФжБНЧзјБъЯЕЃЌЗжБ№аДГіЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЁОНтЮіЁП
(1)жБНгРћгУжсЖдГЦЭМаЮЕФаджЪЕУГіЖдгІЕуЮЛжУНјЖјЕУГіД№АИЃЛ
(2)жБНгРћгУAЕузјБъЕУГіЦНУцжБНЧзјБъЯЕЃЌНјЖјЕУГіИїЕузјБъЃЎ
НтЃК![]() ШчЭМЫљЪОЃК
ШчЭМЫљЪОЃК![]() ЃЌМДЮЊЫљЧѓЃЛ
ЃЌМДЮЊЫљЧѓЃЛ
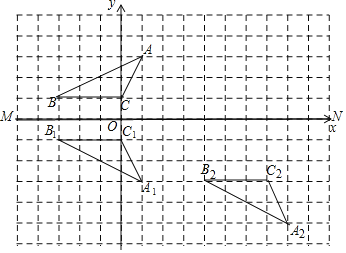
![]() Еу
Еу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЁОЕуОІЁП
ДЫЬтжївЊПМВщСЫжсЖдГЦБфЛЛвдМАЦНвЦБфЛЛЁЂИљОнЕуЕФзјБъНЈСЂЦНУцжБНЧзјБъЯЕЃЌе§ШЗЕУГіЖдгІЕуЮЛжУЪЧНтЬтЙиМќЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
17
ЁОЬтФПЁП![]() МЦЫуЃК
МЦЫуЃК![]() ЃЛ
ЃЛ![]() МЦЫуЃК
МЦЫуЃК![]() ЃЛ
ЃЛ![]() НтЗНГЬзщЃК
НтЗНГЬзщЃК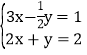 ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаФГжабЇОйааЁАжаЙњУЮаЃдАКУЩљвєЁБИшЪжДѓШќЃЌИпЁЂГѕжаВПИљОнГѕШќГЩМЈЃЌИїбЁГі5УћбЁЪжзщГЩГѕжаДњБэЖгКЭИпжаДњБэЖгВЮМгбЇаЃОіШќЃЎСНИіЖгИїбЁГіЕФ5УћбЁЪжЕФОіШќГЩМЈШчЭМЫљЪОЃЎ

ЃЈ1ЃЉИљОнЭМЪОЬюаДЯТБэЃЛ
ЦНОљЪ§ЃЈЗжЃЉ | жаЮЛЪ§ЃЈЗжЃЉ | жкЪ§ЃЈЗжЃЉ | |
ГѕжаВП | 85 | ||
ИпжаВП | 85 | 100 |
ЃЈ2ЃЉНсКЯСНЖгГЩМЈЕФЦНОљЪ§КЭжаЮЛЪ§ЃЌЗжЮіФФИіЖгЕФОіШќГЩМЈНЯКУЃЛ
ЃЈ3ЃЉМЦЫуСНЖгОіШќГЩМЈЕФЗНВюВЂХаЖЯФФвЛИіДњБэЖгбЁЪжГЩМЈНЯЮЊЮШЖЈЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ14ЗжЃЉХЬНѕКьКЃЬВОАЧјУХЦБМлИё80дЊ/ШЫЃЌОАЧјЮЊЮќв§гЮПЭЃЌЖдУХЦБМлИёНјааЖЏЬЌЙмРэЃЌЗЧНкМйШеДђaелЃЌНкМйШеЦкМфЃЌ10ШЫвдЯТЃЈАќРЈ10ШЫЃЉВЛДђелЃЌ10ШЫвдЩЯГЌЙ§10ШЫЕФВПЗжДђbелЃЌЩшгЮПЭЮЊxШЫЃЌУХЦБЗбгУЮЊyдЊЃЌЗЧНкМйШеУХЦБЗбгУ![]() ЃЈдЊЃЉМАНкМйШеУХЦБЗбгУ
ЃЈдЊЃЉМАНкМйШеУХЦБЗбгУ![]() ЃЈдЊЃЉгыгЮПЭxЃЈШЫЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЃЈдЊЃЉгыгЮПЭxЃЈШЫЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ

ЃЈ1ЃЉa= ЃЌb= ЃЛ
ЃЈ2ЃЉжБНгаДГі![]() ЁЂ
ЁЂ![]() гыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
гыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕМгЮаЁЭѕ6дТ10ШеЃЈЗЧНкМйШеЃЉДјAТУгЮЭХЃЌ6дТ20ШеЃЈЖЫЮчНкЃЉДјBТУгЮЭХЕНКьКЃЬВОАЧјТУгЮЃЌСНЭХЙВМЦ50ШЫЃЌСНДЮЙВИЖУХЦБЗбгУ3040дЊЃЌЧѓAЁЂBСНИіТУгЮЭХИїЖрЩйШЫЃП
ЁОД№АИЁПЃЈ1ЃЉ6ЃЌ8ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() =
=![]() ЃЛЃЈ3ЃЉAЭХга20ШЫЃЌBЭХга30ШЫЃЎ
ЃЛЃЈ3ЃЉAЭХга20ШЫЃЌBЭХга30ШЫЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉгЩКЏЪ§ЭМЯѓЃЌгУЙКЦБПюЪ§Г§вдЖЈМлЕФПюЪ§ЃЌЕУГіaЕФжЕЃЛгУЕк11ШЫЕН20ШЫЕФЙКЦБПюЪ§Г§вдЖЈМлЕФПюЪ§ЃЌЕУГіbЕФжЕЃЛ
ЃЈ2ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓе§БШР§КЏЪ§НтЮіЪНЧѓГі![]() ЃЌЗжxЁм10гыxЃО10ЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓвЛДЮКЏЪ§НтЮіЪНЧѓГі
ЃЌЗжxЁм10гыxЃО10ЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓвЛДЮКЏЪ§НтЮіЪНЧѓГі![]() гыxЕФКЏЪ§ЙиЯЕЪНМДПЩЃЛ
гыxЕФКЏЪ§ЙиЯЕЪНМДПЩЃЛ
ЃЈ3ЃЉЩшAЭХгаnШЫЃЌБэЪОГіBЭХЕФШЫЪ§ЮЊЃЈ50ЉnЃЉЃЌШЛКѓЗж0ЁмnЁм10гыnЃО10СНжжЧщПіЃЌИљОнЃЈ2ЃЉЕФКЏЪ§ЙиЯЕЪНСаГіЗНГЬЧѓНтМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩ![]() ЭМЯѓЩЯЕуЃЈ10ЃЌ480ЃЉЃЌЕУЕН10ШЫЕФЗбгУЮЊ480дЊЃЌЁрa=
ЭМЯѓЩЯЕуЃЈ10ЃЌ480ЃЉЃЌЕУЕН10ШЫЕФЗбгУЮЊ480дЊЃЌЁрa=![]() ЁС10=6ЃЛ
ЁС10=6ЃЛ
гЩy2ЭМЯѓЩЯЕуЃЈ10ЃЌ800ЃЉКЭЃЈ20ЃЌ1440ЃЉЃЌЕУЕН20ШЫжаКѓ10ШЫЗбгУЮЊ640дЊЃЌЁрb=![]() ЁС10=8ЃЛ
ЁС10=8ЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЁпКЏЪ§ЭМЯѓОЙ§ЕуЃЈ0ЃЌ0ЃЉКЭЃЈ10ЃЌ480ЃЉЃЌЁр
ЃЌЁпКЏЪ§ЭМЯѓОЙ§ЕуЃЈ0ЃЌ0ЃЉКЭЃЈ10ЃЌ480ЃЉЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() =48ЃЌЁр
=48ЃЌЁр![]() ЃЛ
ЃЛ
0ЁмxЁм10ЪБЃЌЩш![]() ЃЌЁпКЏЪ§ЭМЯѓОЙ§ЕуЃЈ0ЃЌ0ЃЉКЭЃЈ10ЃЌ800ЃЉЃЌЁр
ЃЌЁпКЏЪ§ЭМЯѓОЙ§ЕуЃЈ0ЃЌ0ЃЉКЭЃЈ10ЃЌ800ЃЉЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() =80ЃЌЁр
=80ЃЌЁр![]() ЃЌxЃО10ЪБЃЌЩш
ЃЌxЃО10ЪБЃЌЩш![]() ЃЌЁпКЏЪ§ЭМЯѓОЙ§ЕуЃЈ10ЃЌ800ЃЉКЭЃЈ20ЃЌ1440ЃЉЃЌЁр
ЃЌЁпКЏЪ§ЭМЯѓОЙ§ЕуЃЈ10ЃЌ800ЃЉКЭЃЈ20ЃЌ1440ЃЉЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЛ
ЃЛ
Ёр![]() =
=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЩшAЭХгаnШЫЃЌдђBЭХЕФШЫЪ§ЮЊЃЈ50ЉnЃЉЃЌЕБ0ЁмnЁм10ЪБЃЌ48n+80ЃЈ50ЉnЃЉ=3040ЃЌНтЕУn=30ЃЈВЛЗћКЯЬтвтЩсШЅЃЉЃЌЕБnЃО10ЪБЃЌ48n+64ЃЈ50ЉnЃЉ+160=3040ЃЌНтЕУn=20ЃЌдђ50Љn=50Љ20=30ЃЎ
Д№ЃКAЭХга20ШЫЃЌBЭХга30ШЫЃЎ
ПМЕуЃК1ЃЎвЛДЮКЏЪ§ЕФгІгУЃЛ2ЃЎЗжЖЮКЏЪ§ЃЛ3ЃЎЗжРрЬжТлЃЛ4ЃЎзлКЯЬтЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
23
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжагавЛЕуЃЌЙ§ИУЕуЗжБ№зїxжсКЭyжсЕФДЙЯпЃЌДЙзуЗжБ№ЪЧAЁЂBЃЌШєгЩИУЕуЁЂдЕуOвдМАСНИіДЙзуЫљзщГЩЕФГЄЗНаЮЕФжмГЄгыУцЛ§ЕФЪ§жЕЯрЕШЃЌдђЮвУЧАбИУЕуНазіЦНУцжБНЧзјБъЯЕжаЕФЦНКтЕуЃЎ
![]() ЧыХаЖЯЯТСаИїЕужаЪЧЦНУцжБНЧзјБъЯЕжаЕФЦНКтЕуЕФЪЧ______ЃЛ
ЧыХаЖЯЯТСаИїЕужаЪЧЦНУцжБНЧзјБъЯЕжаЕФЦНКтЕуЕФЪЧ______ЃЛ![]() ЬюађКХ
ЬюађКХ![]()
![]() ЃЌ
ЃЌ![]() .
.
![]() ШєдкЕквЛЯѓЯожагавЛИіЦНКтЕу
ШєдкЕквЛЯѓЯожагавЛИіЦНКтЕу![]() ЧЁКУдквЛДЮКЏЪ§
ЧЁКУдквЛДЮКЏЪ§![]() ЮЊГЃЪ§
ЮЊГЃЪ§![]() ЕФЭМЯѓЩЯЃЎ
ЕФЭМЯѓЩЯЃЎ
![]() ЧѓmЁЂbЕФжЕЃЛ
ЧѓmЁЂbЕФжЕЃЛ
![]() вЛДЮКЏЪ§
вЛДЮКЏЪ§![]() ЮЊГЃЪ§
ЮЊГЃЪ§![]() гыyжсНЛгкЕуCЃЌЮЪЃКдкетКЏЪ§ЭМЯѓЩЯЃЌЪЧЗёДцдкЕу
гыyжсНЛгкЕуCЃЌЮЪЃКдкетКЏЪ§ЭМЯѓЩЯЃЌЪЧЗёДцдкЕу![]() ЪЙ
ЪЙ![]() ЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌЧвЦНаагкxжсЕФжБЯпЩЯгаЦНКтЕуТ№ЃПШєгаЃЌЧыЧѓГіЦНКтЕуЕФзјБъЃЛШєУЛгаЃЌЫЕУїРэгЩЃЎ
ЃЌЧвЦНаагкxжсЕФжБЯпЩЯгаЦНКтЕуТ№ЃПШєгаЃЌЧыЧѓГіЦНКтЕуЕФзјБъЃЛШєУЛгаЃЌЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦкФЉПМЪдРДСйжЎМЪЃЌЭЌбЇУЧЖМНјШыНєеХЕФИДЯАНзЖЮЃЌЮЊСЫСЫНтЭЌбЇУЧЭэЩЯЕФЫЏУпЧщПіЃЌЯжЖдФъМЖВПЗжЭЌбЇНјааСЫЕїВщЭГМЦЃЌВЂжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃКЃЈЦфжаAДњБэЫЏУпЪБМф8аЁЪБзѓгвЃЌBДњБэЫЏУпЪБМф6аЁЪБзѓгвЃЌCДњБэЫЏУпЪБМф4аЁЪБзѓгвЃЌDДњБэЫЏУпЪБМф5аЁЪБзѓгвЃЌEДњБэЫЏУпЪБМф7аЁЪБзѓгвЃЉЃЌЦфжаЩШаЮЭГМЦЭМжаЁАEЁБЕФдВаФНЧЮЊ90ЁуЃЌЧыФуНсКЯЭГМЦЭМЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЙВГщШЁСЫЁЁЁЁУћЭЌбЇНјааЕїВщЃЌЭЌбЇУЧЕФЫЏУпЪБМфЕФжаЮЛЪ§ЪЧЁЁЁЁаЁЪБзѓгвЃЌВЂНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЧыФуЙРМЦФъМЖУПИібЇЩњЕФЦНОљЫЏУпЪБМфдМЖрЩйаЁЪБЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЁЮCDЃЎЁЯ1=ЁЯ2ЃЌЁЯ3=ЁЯ4ЃЌЪдЫЕУї ADЁЮBEЃЌЧыФуНЋЯТУцНтД№Й§ГЬЬюаДЭъећЃЎ

НтЃКЁпABЁЮCDЃЌ
ЁрЁЯ4= ЃЈ ЃЉ
ЁпЁЯ3=ЁЯ4
ЁрЁЯ3= ЃЈЕШСПДњЛЛЃЉ
ЁпЁЯ1=ЁЯ2
ЁрЁЯ1+ЁЯCAF=ЁЯ2+ЁЯCAE МДЁЯBAE= ЃЎ
ЁрЁЯ3= ЃЈ ЃЉ
ЁрADЁЮBEЃЈ ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com