
����Ŀ���ڱ߳�Ϊ1��������������
![]() ����
����![]() ����ֱ��MN�ԳƵ�
����ֱ��MN�ԳƵ�![]() ��
��
![]() ��
��![]() ����ͼ��ƽ�Ƶõ�
����ͼ��ƽ�Ƶõ�![]() ������A��������
������A��������![]() ʱ���뽨���ʵ���ֱ������ϵ���ֱ�д����
ʱ���뽨���ʵ���ֱ������ϵ���ֱ�д����![]() ��
��![]() ��
��![]() �����꣮
�����꣮
���𰸡���1������������2��![]() ��
��![]() ��
��![]() .
.
��������
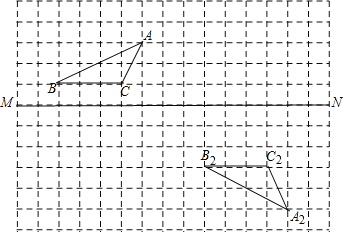
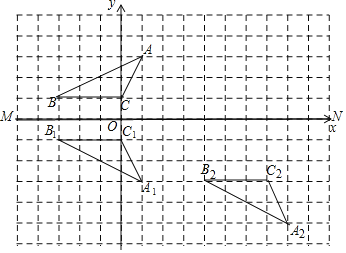
(1)ֱ��������Գ�ͼ�ε����ʵó���Ӧ��λ�ý����ó��𰸣�
(2)ֱ������A������ó�ƽ��ֱ������ϵ�������ó��������꣮
�⣺![]() ��ͼ��ʾ��
��ͼ��ʾ��![]() ����Ϊ����
��������
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���㾦��
������Ҫ��������ԳƱ任�Լ�ƽ�Ʊ任�����ݵ�����꽨��ƽ��ֱ������ϵ����ȷ�ó���Ӧ��λ���ǽ���ؼ���
�����͡������
��������
17
����Ŀ��![]() ���㣺
���㣺![]() ��
��![]() ���㣺
���㣺![]() ��
��![]() �ⷽ���飺
�ⷽ���飺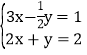 ��
��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=4��BC=3��O�ǡ�ABC�����ģ���OΪԲ�ģ�rΪ�뾶��Բ���߶�AB�н��㣬��r��ȡֵ��Χ�ǣ� ��
A.r��1
B.1��r�� ![]()
C.1��r�� ![]()
D.1��r��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ȤС����15��ͬѧ����һ��Ͷ�������У����ǵijɼ������������ͼ��ʾ����15��ͬѧ����������������λ���ֱ��ǣ�������

A. 10��7 B. 7��7 C. 9��9 D. 9��7
���𰸡�D
�����������������������λ���Ķ���ֱ���н�ɣ�
�⣺������ͳ��ͼ���������ݿɵã�9������6�Σ����ֵĴ�����࣬��������9��
���������ݴ�С�������У����м������7������λ����7��
��ѡD��
���㣺����������ͳ��ͼ����λ����
�����͡���ѡ��
��������
4
����Ŀ����![]() ��
��![]() ����ֱ��
����ֱ��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��![]() �Ĺ�ϵ��
�Ĺ�ϵ��![]() ����
����![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ______��
______��

���𰸡�-1
��������
����A�����������ֱ�߽���ʽ�ó�����m��b�ķ����飬��֮�ɵã�
�⣺������֪![]() ��
��
���![]() ��
��
�ʴ�Ϊ��![]() ��
��
���㾦��
������Ҫ������ֱ���ཻ��ƽ�����⣬����Ĺؼ���������ֱ�ߵĽ�������ض�ͬʱ��������ֱ�߽���ʽ��
�����͡������
��������
11
����Ŀ����ͼ��������ֽƬABCD�У�AB=4��BC=6������ABC��AC�۵���ʹ��B���ڵ�E����CE��AD�ڵ�F�����AFC���������___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2x��m=0������ʵ������
��1����ʵ��m��ȡֵ��Χ��
��2�������̵�����ʵ����Ϊx1��x2 �� ��x1x2=2m2��1����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧϰ��ʽ�˷�ʱ����ʦ�ó������ͺŵĿ�Ƭ����ͼ1��A�Ϳ�Ƭ�DZ߳�Ϊa�������Σ�B�Ϳ�Ƭ�DZ߳�Ϊb�������Σ�C�Ϳ�Ƭ�dz��Ϳ��ֱ�Ϊa��b�ij����Ρ�
��1��ѡȡ1��A�Ϳ�Ƭ��2��C�Ϳ�Ƭ��1��B�Ϳ�Ƭ����ֽ�ϰ���ͼ2�ķ�ʽƴ��һ����Ϊ��a+b���Ĵ������Σ�ͨ����ͬ��ʽ��ʾ�������ε�������ɵõ��˷���ʽ��______________



��2������ͼ1�е�8��C�ͳ����ο�Ƭ����ƴ����ͼ3��ʾ�ij����Σ����Ŀ�Ϊ20cm���������ÿ�鳤���ε����
��3��ѡȡ1��A�Ϳ�Ƭ��3��C�Ϳ�Ƭ��ͼ4�ķ�ʽ���ص��ط��ڳ�����DEFG����ڣ���֪GF�ij��ȹ̶����䣬DG�ij��ȿ��Ա仯��ͼ������Ӱ���֣������Σ�������ֱ��ʾΪS1��S2����S=S2-S1����a��b����_________ʱ��SΪ��ֵ���Ҷ�ֵΪ___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ļ���Ʒ�̵깺�����������20�������ۺ��ۼ����±���ʾ��ȫ�������������260Ԫ.
��1�������������������ٸ���
��2������6����������������ۼ��������������ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B�������4ǧ�ף�����8��00���״�A�س������е�B�أ�8��20�Ҵ�B�س��������г���A�أ��ס���������A�صľ��루ǧ�ף�������õ�ʱ�䣨�֣�֮��Ĺ�ϵ��ͼ��ʾ����ͼ�е���Ϣ��֪���ҵ���A�ص�ʱ��Ϊ____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ȫ�ȵĺ�30����60���ǵ����ǰ�ADE�����ǰ�ABC������һ�𣬡�DEA����ACB��90������DAE����ABC��30����E��A��C������һ��ֱ���ϣ�����BD��ȡBD�е�M������ME��MC�����ж���EMC����״����˵�����ɣ�
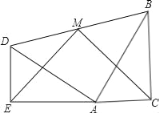
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com