
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
A.r≥1
B.1≤r≤ ![]()
C.1≤r≤ ![]()
D.1≤r≤4
【答案】C
【解析】解:作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,连接OA、OB,如图所示
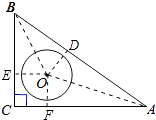
则四边形OECF是正方形,
∴OF=CF=OE=CE,
∵∠C=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
∵O是△ABC的内心,
∴CE=CF=OF=OE= ![]() (AC+BC﹣AB)=1,
(AC+BC﹣AB)=1,
∴AF=AC﹣CF=3,BE=BC﹣CE=2,
∴OA= ![]() ,OB=
,OB= ![]() =
= ![]() ,
,
当r=1时,以O为圆心,r为半径的圆与线段AB有唯一交点;
当1<r≤ ![]() 时,以O为圆心,r为半径的圆与线段AB有两个交点;
时,以O为圆心,r为半径的圆与线段AB有两个交点;
当 ![]() <r≤
<r≤ ![]() 时,以O为圆心,r为半径的圆与线段AB有1个交点;
时,以O为圆心,r为半径的圆与线段AB有1个交点;
∴以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是1≤r≤ ![]() ;
;
所以答案是:C
【考点精析】掌握直线与圆的三种位置关系和三角形的内切圆与内心是解答本题的根本,需要知道直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0; ②当x>1时,y的值随x值的增大而减小;
③当 ![]() 时,
时, ![]() ; ④3是方程ax2+(b﹣1)x+c=0的一个根.
; ④3是方程ax2+(b﹣1)x+c=0的一个根.
其中正确的结论是(填正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本1.4有这样一道例题:
问题4:用一根长22cm的铁丝:
(1)能否围成面积是30cm2的矩形?
(2)能否围成面积是32cm2的矩形?
据此,一位同学提出问题:“用这根长22cm的铁丝能否围成面积最大的矩形?若能围成,求出面积最大值;若不能围成,请说明理由.”请你完成该同学提出的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,则图中面积相等的平行四边形有( )

A. 3对 B. 2对 C. 1对 D. 0对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=BC=5,AB=5![]() ,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.
,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:BM∥DN;
(2)求证:四边形MPNQ是菱形;
(3)矩形ABCD的边长AB与AD满足什么数量关系时四边形MPNQ为正方形,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,A,B,C,D四点共圆,过点C的切线CE∥BD,与AB的延长线交于点E.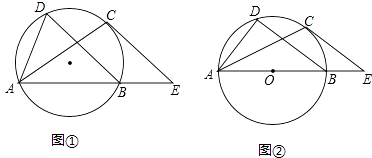
(1)求证:∠BAC=∠CAD;
(2)如图②,若AB为⊙O的直径,AD=6,AB=10,求CE的长;
(3)在(2)的条件下,连接BC,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的正方形网格中
![]() 作出
作出![]() 关于直线MN对称的
关于直线MN对称的![]() ;
;
![]() 若
若![]() 经过图形平移得到
经过图形平移得到![]() ,当点A的坐标是
,当点A的坐标是![]() 时,请建立适当的直角坐标系,分别写出点
时,请建立适当的直角坐标系,分别写出点![]() ,
,![]() ,
,![]() 的坐标.
的坐标.
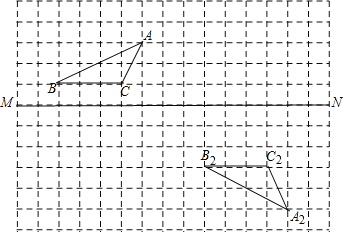
【答案】(1)见解析;(2)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)直接利用轴对称图形的性质得出对应点位置进而得出答案;
(2)直接利用A点坐标得出平面直角坐标系,进而得出各点坐标.
解:![]() 如图所示:
如图所示:![]() ,即为所求;
,即为所求;
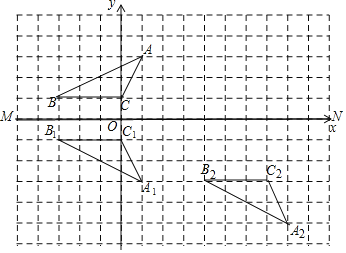
![]() 点
点![]() ,
,![]() ,
,![]() .
.
【点睛】
此题主要考查了轴对称变换以及平移变换、根据点的坐标建立平面直角坐标系,正确得出对应点位置是解题关键.
【题型】解答题
【结束】
17
【题目】![]() 计算:
计算:![]() ;
;![]() 计算:
计算:![]() ;
;![]() 解方程组:
解方程组: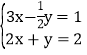 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com