
【题目】已知:如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:BM∥DN;
(2)求证:四边形MPNQ是菱形;
(3)矩形ABCD的边长AB与AD满足什么数量关系时四边形MPNQ为正方形,请说明理由.

【答案】(1)详见解析;(2)详见解析;(3)当AB=![]() AD时,四边形MPNQ为正方形,理由详见解析.
AD时,四边形MPNQ为正方形,理由详见解析.
【解析】
(1)因为M,N分别是AD,BC的中点,由矩形的性质可得DM=BN,DM∥BN,利用平行四边形的判定和性质可得结论;
(2)由四边形DMBN是平行四边形,求出BM=DN,BM∥DN,求出三角形MPNQ是平行四边形,根据直角三角形斜边上中线性质求出MQ=NQ,根据菱形判定推出即可.
(3)根据正方形的性质进行解答即可.
证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵M、N分别AD、BC的中点,
∴DM=BN,
∴四边形DMBN是平行四边形;
∴BM∥DN;
(2)∵四边形DMBN是平行四边形,
∴BM=DN,BM∥DN,
∵P、Q分别BM、DN的中点,
∴MP=NQ,MP∥NQ,
∴四边形MPNC是平行四边形,
连接MN,
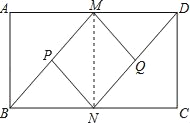
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵M、N分别AD、BC的中点,
∴DM=CN,
∴四边形DMNC是矩形,
∴∠DMN=∠C=90°,
∵Q是DN中点,
∴MQ=NQ,
∴四边形MPNQ是菱形.
(3)当AB=![]() AD时,四边形MPNQ为正方形,
AD时,四边形MPNQ为正方形,
理由:∵AB=![]() AD,
AD,
∴AB=AM,
∴矩形ABNM是正方形,
∵P为正方形ABNM对角线BM的中点,
∴∠NPM=90°,
∵四边形MPNQ是菱形,
∴四边形MPNQ是正方形.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】问题探究:小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请你解决相关问题:
![]() 在函数
在函数![]() 中,自变量x可以是任意实数;
中,自变量x可以是任意实数;
![]() 如表y与x的几组对应值:
如表y与x的几组对应值:
X |
|
|
|
|
| 0 | 1 | 2 | 3 | 4 |
|
Y |
|
| 0 | 1 | 2 | 3 | 2 | 1 | a |
|
|
![]() ______;
______;
![]() 若
若![]() ,
,![]() 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则![]() ______;
______;
![]() 如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
![]() 该函数有______
该函数有______![]() 填“最大值”或“最小值”
填“最大值”或“最小值”![]() ;并写出这个值为______;
;并写出这个值为______;
![]() 求出函数图象与坐标轴在第二象限内所围成的图形的面积;
求出函数图象与坐标轴在第二象限内所围成的图形的面积;
![]() 观察函数
观察函数![]() 的图象,写出该图象的两条性质.
的图象,写出该图象的两条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
A.r≥1
B.1≤r≤ ![]()
C.1≤r≤ ![]()
D.1≤r≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:
观察下面由※组成的图案和算式,解答问题:

1+3=22=4
1+3+5=32=9
1+3+5+7=42=16
1+3+5+7+9=52=25
(1)猜想1+3+5+7+9+…+29= = ;
(2)猜想1+3+5+7+9+…+(2n﹣1)+(2n+1)= = ;
(3)用上述规律计算:41+43+45+…+77+79.
查看答案和解析>>
科目:初中数学 来源: 题型:
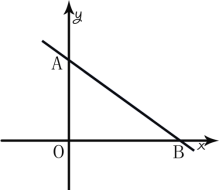
【题目】如图,直线MN与x轴、y轴分别相交于B、A两点,OA,OB的长满足式子![]()
(1)求A,B两点的坐标;
(2)若点O到AB的距离为![]() ,求线段AB的长;
,求线段AB的长;
(3)在(2)的条件下,x轴上是否存在点P,使ΔABP使以AB为腰的等腰三角形,若存在请直接写出满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.

(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球兴趣小组有15名同学,在一次投篮比赛中,他们的成绩如右面的条形图所示.这15名同学进球数的众数和中位数分别是( )

A. 10,7 B. 7,7 C. 9,9 D. 9,7
【答案】D
【解析】试题根据众数与中位数的定义分别进行解答即可.
解:由条形统计图给出的数据可得:9出现了6次,出现的次数最多,则众数是9;
把这组数据从小到达排列,最中间的数是7,则中位数是7.
故选D.
考点:众数;条形统计图;中位数.
【题型】单选题
【结束】
4
【题目】点![]() 和
和![]() 都在直线
都在直线![]() 上,且
上,且![]() ,则
,则![]() 与
与![]() 的关系是
的关系是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育文化用品商店购进篮球和排球共20个,进价和售价如下表所示,全部销售完后共获利润260元.
(1)购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相等?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com