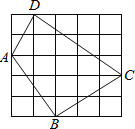
【题目】如图，小方格都是边长为1的正方形
（1）求
的长度．
（2）用勾股定理的知识证明：
．
【答案】（1）AB=
，BC= ；（2）见解析.
【解析】
（1）如图1，分别在Rt△AEB和RtBFC中分别由勾股定理可求得AB和BC的长；
（2）如图2，连接AC，在Rt△ACG中由勾股定理可求得AC，则可得到AB2+BC2=AC2，可证得△ABC为直角三角形，即可得结论．
(1) 解：如图1，
在Rt△ABE中，AE=3，BE=2，
∴AB=
= ，
在Rt△BCF中，BF=3，CF=2，
∴BC=
= ；
(2)证明：如图2，连接AC，
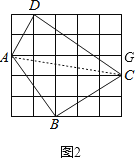
在Rt△ACG中，AG=5，CG=1，
∴AC=
，
结合(1)可得
=
∴△ABC是以AC为斜边的直角三角形，
∴∠ABC=90°.
故答案为：（1）AB= ，BC= ；（2）见解析.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A(-2，2)，B(0，5)，C(0，2).
(1)将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形.
(2)平移△ABC，使点A的对应点A2坐标为(-2，-6)，请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD中，∠B＝30°，AB≠BC ，将△ABC沿AC翻折至△AB′C ，连结B ′D. 若 
，∠AB ′D＝75°，则BC= ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：
①ac＜0； ②当x＞1时，y的值随x值的增大而减小；
③当 
时， 
； ④3是方程ax2+（b﹣1）x+c=0的一个根.
其中正确的结论是（填正确结论的序号）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学校准备租用一批汽车，现有甲、乙两种大客车，甲种客车每辆载客量45人，乙种客车每辆载客量30人，已知1辆甲种客车和3辆乙种客车共需租金1240元，3辆甲种客车和2辆乙种客车共需租金1760元．
（1）求1辆甲种客车和1辆乙种客车的租金分别是多少元？
（2）学校计划租用甲、乙两种客车共8辆，送330名师生集体外出活动，最节省的租车费用是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等边△ABC中，BD⊥AC于点D，AD＝3.5cm，点P、Q分别为AB、AD上的两个定点且BP＝AQ＝2cm，若在BD上有一动点E使PE＋QE最短，则PE＋QE的最小值为_____cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y=k1x+b与反比例函数y= 
的图象交于A（2，m），B（-3，﹣2）两点.
（1）求m的值；
（2）根据所给条件，请直接写出不等式k1x+b＞ 的解集；
（3）若P（p，y1），Q（﹣2，y2）是函数y= 图象上的两点， 且y1＞y2 ， 求实数p的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在矩形ABCD中，M、N分别是AD、BC的中点，P、Q分别是BM、DN的中点．
（1）求证：BM∥DN；
（2）求证：四边形MPNQ是菱形；
（3）矩形ABCD的边长AB与AD满足什么数量关系时四边形MPNQ为正方形，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
