
【题目】问题探究:小明根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请你解决相关问题:
![]() 在函数
在函数![]() 中,自变量x可以是任意实数;
中,自变量x可以是任意实数;
![]() 如表y与x的几组对应值:
如表y与x的几组对应值:
X |
|
|
|
|
| 0 | 1 | 2 | 3 | 4 |
|
Y |
|
| 0 | 1 | 2 | 3 | 2 | 1 | a |
|
|
![]() ______;
______;
![]() 若
若![]() ,
,![]() 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则![]() ______;
______;
![]() 如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
如图,在平面直角坐标系中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
![]() 该函数有______
该函数有______![]() 填“最大值”或“最小值”
填“最大值”或“最小值”![]() ;并写出这个值为______;
;并写出这个值为______;
![]() 求出函数图象与坐标轴在第二象限内所围成的图形的面积;
求出函数图象与坐标轴在第二象限内所围成的图形的面积;
![]() 观察函数
观察函数![]() 的图象,写出该图象的两条性质.
的图象,写出该图象的两条性质.
【答案】(2)![]() 0;
0;![]() ;(3)①最大值,3;②
;(3)①最大值,3;②![]() ;③函数图象为轴对称图形,对称轴为y轴;当
;③函数图象为轴对称图形,对称轴为y轴;当![]() 时,y随x的增大而增大,当
时,y随x的增大而增大,当![]() 时,y随x增大而减小.
时,y随x增大而减小.
【解析】
![]() 将
将![]() 代入函数解析式即可求得a;
代入函数解析式即可求得a;
![]() 当
当![]() 时,根据函数解析式可求得b;
时,根据函数解析式可求得b;
![]() 根据题意画出函数图象,根据图象特征即可求得题目所求.
根据题意画出函数图象,根据图象特征即可求得题目所求.
解:![]() 当
当![]() 时,求得
时,求得![]() ;
;
![]() 由题意,当
由题意,当![]() 时,得
时,得![]() ,解得:
,解得:![]() 或
或![]() ,所以
,所以![]() .
.
![]() 函数图象如下图所示:
函数图象如下图所示:
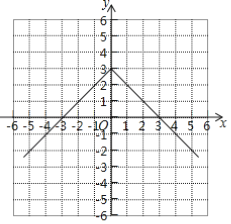
![]() 由图知,该函数有最大值3;
由图知,该函数有最大值3;
![]() 由图知,函数图象与x轴负半轴的交点为
由图知,函数图象与x轴负半轴的交点为![]() ,与y轴正半轴的交点为
,与y轴正半轴的交点为![]() ,
,
因此函数图象在第二象限内所围成的图形的面积为:![]() ,
,
![]() 由图象知可知函数
由图象知可知函数![]() 有如下性质:
有如下性质:
函数图象为轴对称图形,对称轴为y轴;当![]() 时,y随x的增大而增大,当
时,y随x的增大而增大,当![]() 时,y随x增大而减小.
时,y随x增大而减小.
故答案为:(2)![]() 0;
0;![]() ;(3)①最大值,3;②
;(3)①最大值,3;②![]() ;③函数图象为轴对称图形,对称轴为y轴;当
;③函数图象为轴对称图形,对称轴为y轴;当![]() 时,y随x的增大而增大,当
时,y随x的增大而增大,当![]() 时,y随x增大而减小.
时,y随x增大而减小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=30°,AB≠BC ,将△ABC沿AC翻折至△AB′C ,连结B ′D. 若 ![]() ,∠AB ′D=75°,则BC= .
,∠AB ′D=75°,则BC= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y= ![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b> ![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y= ![]() 图象上的两点, 且y1>y2 , 求实数p的取值范围.
图象上的两点, 且y1>y2 , 求实数p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建全国卫生城市,我市某单位全体职工利用周末休息时间参加社会公益活动,并对全体职工参加公益活动的时间![]() 单位:天
单位:天![]() 进行了调查统计,根据调查结果绘制了如图所示的两幅不完整的统计图,根据信息回答下列问题:
进行了调查统计,根据调查结果绘制了如图所示的两幅不完整的统计图,根据信息回答下列问题:
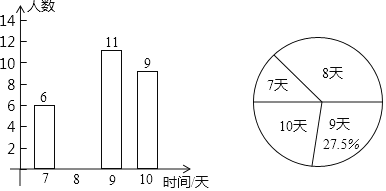
![]() 该单位职工共有______名;
该单位职工共有______名;
![]() 补全条形统计图;
补全条形统计图;
![]() 职工参加公益活动时间的众数是______天,中位数是______天;
职工参加公益活动时间的众数是______天,中位数是______天;
![]() 职工参加公益活动时间总计达到多少天?
职工参加公益活动时间总计达到多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本1.4有这样一道例题:
问题4:用一根长22cm的铁丝:
(1)能否围成面积是30cm2的矩形?
(2)能否围成面积是32cm2的矩形?
据此,一位同学提出问题:“用这根长22cm的铁丝能否围成面积最大的矩形?若能围成,求出面积最大值;若不能围成,请说明理由.”请你完成该同学提出的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,则图中面积相等的平行四边形有( )

A. 3对 B. 2对 C. 1对 D. 0对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:BM∥DN;
(2)求证:四边形MPNQ是菱形;
(3)矩形ABCD的边长AB与AD满足什么数量关系时四边形MPNQ为正方形,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com