
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,BF交AC于G,连接CF.
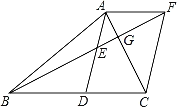
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,①试判断四边形ADCF的形状,并证明你的结论;
②若AB=8,BD=5,直接写出线段AG的长 .
【答案】(1)详见解析;(2)①四边形ADCF是菱形;详见解析;②2
【解析】
(1)由平行线证明三角形全等所缺少的条件,再根据三角形全等的判定方法证明三角形全等;
(2)①先证四边形ADCF是平行四边形,再证明邻边相等,便可得出结论;
②证明△AFG∽△CBG,得出AG与AC的比例关系,进而由直角三角形的性质求得AC,便可得AG.
(1)∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
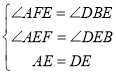 ,
,
∴△AEF≌△DEB(AAS);
(2)①四边形ADCF是菱形,
理由如下:∵△AEF≌△DEB,
∴AF=BD,
∵BD=DC,
∴AF=DC=![]() BC,
BC,
又AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,AD是BC边上的中线,
∴AD=DC,
∴四边形ADCF是菱形;
②∵AF∥BC,
∴△AFG∽△CBG,
∴![]()
∴![]()
∴AG=![]() ,
,
∵BD=5,AD是BC边上的中线,
∴BC=2BD=10,
∵∠BAC=90°,AB=8,
∴AC=![]() ,
,
∴AG=![]() =2,
=2,
故答案为2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
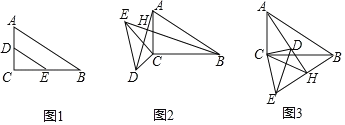
【题目】已知:已知Rt△ABC中,∠ACB=90°,D、E分别是AC、BC上的点,连DE,且![]() ,tanB
,tanB![]() ,如图1.
,如图1.
(1)如图2,将△CDE绕C点旋转,连AD、BE交于H,求证:AD⊥BE;
(2)如图3,当△CDE绕C点旋转过程中,当CH![]() 时,求
时,求![]() AH﹣BH的值;
AH﹣BH的值;
(3)若CD=1,当△CDE绕C点旋转过程中,直接写出AH的最大值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
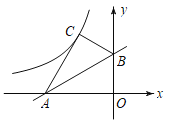
【题目】如图,已知直线![]() 与x轴,y轴分别交于点A,B,将△ABO沿直线AB翻折后得到△ABC,若反比例函数
与x轴,y轴分别交于点A,B,将△ABO沿直线AB翻折后得到△ABC,若反比例函数![]() (x<0)的图象经过点C,则k=______.
(x<0)的图象经过点C,则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
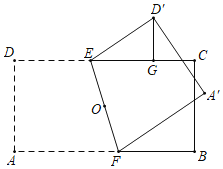
【题目】如图,点O是矩形ABCD的对角线的交点,AB=15,BC=8,直线EF经过点O,分别与边CD,AB相交于点E,F(其中0<DE<![]() ).现将四边形ADEF沿直线EF折叠得到四边形A′D′EF,点A,D的对应点分别为A′,D′,过D′作D′G⊥CD于点G,则线段D′G的长的最大值是_____,此时折痕EF的长为_____.
).现将四边形ADEF沿直线EF折叠得到四边形A′D′EF,点A,D的对应点分别为A′,D′,过D′作D′G⊥CD于点G,则线段D′G的长的最大值是_____,此时折痕EF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣![]() x+3的图象与反比例函数y=
x+3的图象与反比例函数y=![]() 的图象相交于A(m,6),B两点.
的图象相交于A(m,6),B两点.
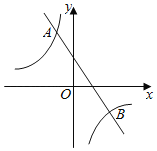
(1)求反比例函数的表达式及点B的坐标;
(2)点P在x轴上,连接AP,BP,若△ABP的面积为18,求满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
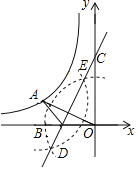
【题目】如图,点A在双曲线y=![]() (k<0)上,连接OA,分别以点O和点A为圆心,大于
(k<0)上,连接OA,分别以点O和点A为圆心,大于![]() OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
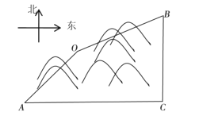
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起,高铁大大缩短了时空距离,改变了人们的出行方式,如图![]() 两地被大山阻隔,由
两地被大山阻隔,由![]() 地到
地到![]() 地需要绕行
地需要绕行![]() 地,若打通穿山隧道由
地,若打通穿山隧道由![]() 地到
地到![]() 地,再由
地,再由![]() 地到
地到![]() 地可大大缩短路程.
地可大大缩短路程.![]() ,
,![]() ,
,![]() ,
,![]() 公里,
公里,![]() 公里,求隧道打通后与打通前相比,从
公里,求隧道打通后与打通前相比,从![]() 地到
地到![]() 地的路程将约缩短多少公里?(参考数据:
地的路程将约缩短多少公里?(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
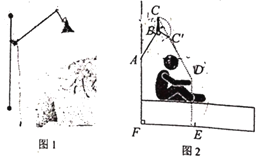
【题目】如图1是一款创意型壁灯,示意图如图2所示,∠BAF=150°,灯臂BC=0.2米,不使用时BC‖AF,人在床上阅读时,将![]() 绕点B旋转至
绕点B旋转至![]() ,
,![]() ,书本到地面距离DE=1米,C,
,书本到地面距离DE=1米,C,![]() ,D三点恰好在同一直线上,且
,D三点恰好在同一直线上,且![]() ,则此时固定点A到地面的距离
,则此时固定点A到地面的距离![]() ________米.
________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数![]() 在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1。直线l过O、E两点,则tan∠EOC的值为( )
在第一象限的图象经过顶点A(m,m+3)和CD上的点E,且OB-CE=1。直线l过O、E两点,则tan∠EOC的值为( )

A. ![]() B. 5 C.
B. 5 C. ![]() D. 3
D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com