
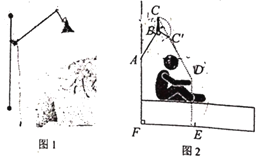
【题目】如图1是一款创意型壁灯,示意图如图2所示,∠BAF=150°,灯臂BC=0.2米,不使用时BC‖AF,人在床上阅读时,将![]() 绕点B旋转至
绕点B旋转至![]() ,
,![]() ,书本到地面距离DE=1米,C,
,书本到地面距离DE=1米,C,![]() ,D三点恰好在同一直线上,且
,D三点恰好在同一直线上,且![]() ,则此时固定点A到地面的距离
,则此时固定点A到地面的距离![]() ________米.
________米.
【答案】1.4
【解析】
延长AB与CD交于G,作AH⊥AF,交CD于H,作HP‖AF,作DE⊥AE,DI⊥AF,BK⊥CD,构造等边三角形AGH和直角三角形BGC'和直角三角形FOD,然后利用三角函数关系求出DH,再求出OH,进而求出AF.
如图,延长AB与CD交于G,作AH⊥AF,交CD于H,作HP‖AF,作DE⊥AE,DI⊥AF,BK⊥CD,
因为∠BAF=150°
所以∠QAB=∠CBG=30°
∠ABC=∠BAF=150°
因为AB⊥BC
所以∠ABC=90°
所以∠CBC'=360°-150°-90°=120°,
∠BAH=60°
因为BC=BC'=0.2(米)
所以∠C=∠BC'C=![]()
所以∠C=∠CBG=30°
CC'=2CK=2BCcos30°=![]() (米)
(米)
所以BG=CG=BC'tan30°=0.2![]() (米)
(米)
∠BGC'=30°×2=60°
所以∠BGC'=∠BAH=60°
所以△AGH是等边三角形
所以AG=GH
设AB=x,则GH=AG=![]() (米) ,C'D=AB+CC'=
(米) ,C'D=AB+CC'=![]() ,CD=
,CD=![]() (米)
(米)
所以DH=CD-GH-CH
=![]() -
-![]() (米)
(米)
在Rt△HOD中,∠DHO=30°
所以OH=HDcos30°=![]() (米)
(米)
所以AF=AI+IF=OH+DE=1.4(米)
故答案为:1.4


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
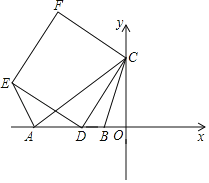
【题目】如图,在平面直角坐标系中,点A、B在x轴上,点C在y轴上,AB=BC=5,AC=8,D为线段AB上一动点,以CD为边在x轴上方作正方形CDEF,连接AE.
(1)若点B的坐标为(m,0),则m= ;
(2)当BD= 时,EA⊥x轴;
(3)当点D由点B运动到点A过程中,点F经过的路径长为 ;
(4)当△ADE面积最大时,求出BD的长及△ADE面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
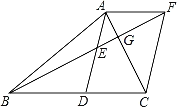
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,BF交AC于G,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,①试判断四边形ADCF的形状,并证明你的结论;
②若AB=8,BD=5,直接写出线段AG的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
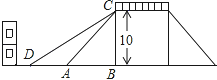
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
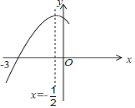
【题目】如图,抛物线![]() =
=![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() ,结合图象分析下列结论:
,结合图象分析下列结论:
① ![]() ; ②
; ② ![]() ;
;
③ ![]() >0; ④当
>0; ④当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
⑤ ![]() ≤
≤![]() (m为实数),其中正确的结论有( )
(m为实数),其中正确的结论有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.

(1)分别写出两个印刷厂的收费![]() ,
,![]() (元)与印制数量
(元)与印制数量![]() (份)之间的关系式(不用写出自变量的取值范围);
(份)之间的关系式(不用写出自变量的取值范围);
(2)在同一坐标系内画出它们的图象,并求出当印制多少份宣传材料,两个印刷厂的印制费用相同?此时费用为多少?
(3)结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印制省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
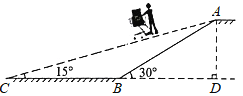
【题目】某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为30°;改造后的斜坡式自动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度,(结果精确到0.lm.温馨提示:sin15°≈0.26,cosl5°≈0.97,tan15°≈0.27)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com