
【题目】如图,抛物线![]() =
=![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() ,结合图象分析下列结论:
,结合图象分析下列结论:
① ![]() ; ②
; ② ![]() ;
;
③ ![]() >0; ④当
>0; ④当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
⑤ ![]() ≤
≤![]() (m为实数),其中正确的结论有( )
(m为实数),其中正确的结论有( )
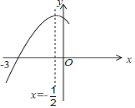
A.2个B.3个C.4个D.5个
【答案】B
【解析】
根据题意和函数图象中的数据,利用二次函数的性质可以判断各个小题中的结论是否正确,从而可以解答本题.
∵抛物线y=ax2+bx+c(a≠0)与x轴交于点(-3,0),其对称轴为直线![]() ,
,
∴抛物线y=ax2+bx+c(a≠0)与x轴交于点(-3,0)和(2,0),且![]() =
=![]() ,
,
∴a=b,
由图象知:a<0,c>0,b<0,
∴abc>0,故结论①正确;
∵抛物线y=ax2+bx+c(a≠0)与x轴交于点(-3,0),
∴9a-3b+c=0,
∵a=b,
∴c=-6a,
∴3a+c=-3a>0,故结论②正确;
∵当![]() 时,y=
时,y=![]() >0,
>0,
∴![]() <0,故结论③错误;
<0,故结论③错误;
当x<![]() 时,y随x的增大而增大,当
时,y随x的增大而增大,当![]() <x<0时,y随x的增大而减小,故结论④错误;
<x<0时,y随x的增大而减小,故结论④错误;
∵a=b,
∴![]() ≤
≤![]() 可换成
可换成![]() ≤
≤![]() ,
,
∵a<0,
∴可得![]() ≥-1,
≥-1,
即4m2+4m+1≥0
(2m+1)2≥0,故结论⑤正确;
综上:正确的结论有①②⑤,
故选:B.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=![]() (k<0)上,连接OA,分别以点O和点A为圆心,大于
(k<0)上,连接OA,分别以点O和点A为圆心,大于![]() OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
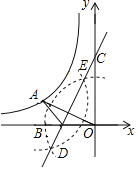
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止,设P、Q同时出发t秒时,BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示(其中曲线OG为抛物线的一部分,其余各部分均为线段)所示,则下列结论:①BEBC;②当t6秒时,ABE PQB;③点P运动了18秒;④当t![]() 秒时,ABE∽QBP.其中正确的是( ).
秒时,ABE∽QBP.其中正确的是( ).
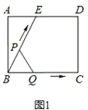
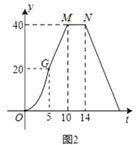
A.①②B.①③④C.③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
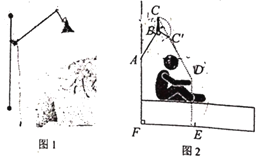
【题目】如图1是一款创意型壁灯,示意图如图2所示,∠BAF=150°,灯臂BC=0.2米,不使用时BC‖AF,人在床上阅读时,将![]() 绕点B旋转至
绕点B旋转至![]() ,
,![]() ,书本到地面距离DE=1米,C,
,书本到地面距离DE=1米,C,![]() ,D三点恰好在同一直线上,且
,D三点恰好在同一直线上,且![]() ,则此时固定点A到地面的距离
,则此时固定点A到地面的距离![]() ________米.
________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C = 90°,以AC为直径的⊙O交AB于点D,连接OD,点E在BC上, B E=DE.

(1)求证:DE是⊙O的切线;
(2)若BC=6,求线段DE的长;
(3)若∠B=30°,AB =8,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.
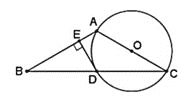
(1)求证:DE是⊙O的切线;
(2)若DE= ![]() ,∠C=30°,求
,∠C=30°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
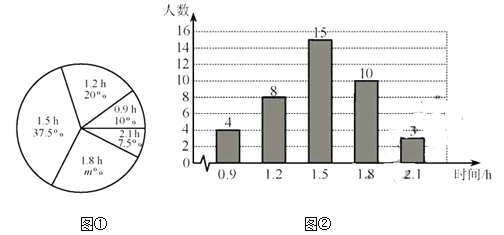
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
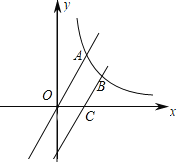
【题目】如图,已知函数y=2x与反比例函数y=![]() (x>0)的图象交于点A,将y=2x的图象向下平移6个单位后与反比例函数y═
(x>0)的图象交于点A,将y=2x的图象向下平移6个单位后与反比例函数y═![]() (x>0)交于点B,与x轴交于点C,若OA=2BC,则k=_____.
(x>0)交于点B,与x轴交于点C,若OA=2BC,则k=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com