
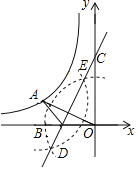
【题目】如图,点A在双曲线y=![]() (k<0)上,连接OA,分别以点O和点A为圆心,大于
(k<0)上,连接OA,分别以点O和点A为圆心,大于![]() OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
OA的长为半径作弧,两弧相交于D,E两点,直线DE交x轴于点B,交y轴于点C(0,3),连接AB.若AB=1,则k的值为_____.
【答案】﹣![]() .
.
【解析】
BC交OA于H,如图,利用基本作图得到CB垂直平分OA,则BO=BA=1,AH=OH,在Rt△OCB中先利用勾股定理计算出CB,再利用面积法计算出OH=![]() ,则OA=
,则OA=![]() ,设A(m,n),根据两点间的距离公式得到(m+1)2+n2=12,m2+n2=(
,设A(m,n),根据两点间的距离公式得到(m+1)2+n2=12,m2+n2=(![]() )2,解关于m、n的方程组得到A
)2,解关于m、n的方程组得到A![]() ,然后利用反比例函数图像上点的坐标特征求k的值.
,然后利用反比例函数图像上点的坐标特征求k的值.
BC交OA于H,如图,
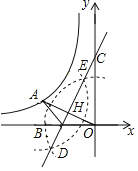
由作法得CB垂直平分OA,
∴BO=BA=1,AH=OH,∠OBH=90°,
∴B(﹣1,0),
在Rt△OCB中,
∵C(0,3),
∴OC=3,
∴CB=![]() =
=![]() ,
,
∵![]() ×OH×BC=
×OH×BC=![]() ×OB×OC,
×OB×OC,
∴OH=![]() ,
,
∴OA=2OH=![]() ,
,
设A(m,n),则(m+1)2+n2=12,m2+n2=(![]() )2,
)2,
解得m=![]() ,n=
,n=![]() ,
,
∴A ![]() ,
,
把A![]() 代入
代入![]() 得k=
得k=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
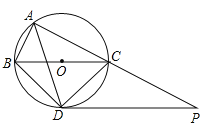
(1)求证:PD是⊙O的切线;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() ,求线段DP的长.
,求线段DP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
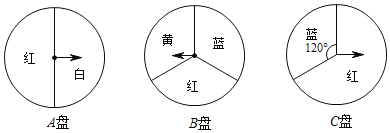
【题目】小颖为学校联欢会设计了一个“配紫色”游戏:如图是三个可以自由转动的转盘,A盘和B盘被分成面积相等的几个扇形.游戏者同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)若游戏者同时转动A盘和B盘,请利用画树状图或列表的方法,求他获胜的概率;
(2)若游戏者同时转动B盘和C盘,请直接写出他获胜的概率,不必写出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,BF交AC于G,连接CF.
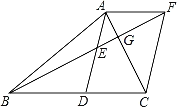
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,①试判断四边形ADCF的形状,并证明你的结论;
②若AB=8,BD=5,直接写出线段AG的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,AB=10,AC=BC=13,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF⊥AC,于点F,交CB的延长线于点E.
(1)求证:DF是⊙O的切线;
(2)求cos∠ADF的值.
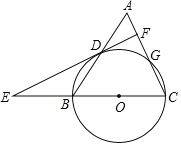
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() =
=![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() ,结合图象分析下列结论:
,结合图象分析下列结论:
① ![]() ; ②
; ② ![]() ;
;
③ ![]() >0; ④当
>0; ④当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
⑤ ![]() ≤
≤![]() (m为实数),其中正确的结论有( )
(m为实数),其中正确的结论有( )
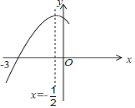
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.点E为圆上一点,∠ECD=15°,将![]() 沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
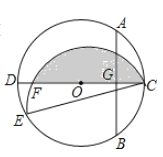
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com