
把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
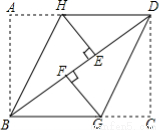
(1)证明见解析;(2)3cm.
【解析】
试题分析:(1)先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠ABH=∠EBH,∠FDG=∠CDG,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG;
(2)先根据勾股定理得出BD的长,进而得出BF的长,由图形翻折变换的性质得出CG=FG,设FG=x,则BG=8-x,再利用勾股定理即可求出x的值.
试题解析:(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,∠ABD=∠BDC,
∵△BEH是△BAH翻折而成,
∴∠ABH=∠EBH,∠A=∠HEB=90°,AB=BE,
∵△DGF是△DGC翻折而成,
∴∠FDG=∠CDG,∠C=∠DFG=90°,CD=DF,
∴∠DBH=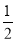 ∠ABD,∠BDG=
∠ABD,∠BDG=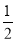 ∠BDC,
∠BDC,
∴∠DBH=∠BDG,
∴△BEH与△DFG中,
∠HEB=∠DFG,BE=DF,∠DBH=∠BDG,
∴△BEH≌△DFG,
(2)【解析】
∵四边形ABCD是矩形,AB=6cm,BC=8cm,
∴AB=CD=6cm,AD=BC=8cm,
∴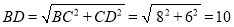 ,
,
∵由(1)知,FD=CD,CG=FG,
∴BF=10-6=4cm,
设FG=x,则BG=8-x,
在Rt△BGF中,
BG2=BF2+FG2,即(8-x)2=42+x2,
解得x=3,即FG=3cm.
考点:1.翻折变换(折叠问题);2.勾股定理;3.矩形的性质.


科目:初中数学 来源:2015届江西省九年级上学期入学考试数学试卷(解析版) 题型:解答题
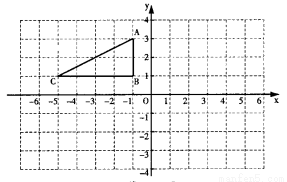
△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向右平移6个单位得到△A1B1C1,请画出△A1B1C1;并写出点C1的坐标;
(2)将△ABC绕原点O旋转180°得到△A2B2C2,请画出△A2B2C2.
查看答案和解析>>
科目:初中数学 来源:2015届江西省八年级下学期第一次月考数学试卷(解析版) 题型:选择题
等腰三角形的一边为4,另一边为9,则这个三角形的周长为 ( )
A、17 B、22 C、13 D、17或22
查看答案和解析>>
科目:初中数学 来源:2015届江苏省八年级下学期期中联考数学试卷(解析版) 题型:填空题
在九张质地都相同的卡片上分别写有数字-4,-3,-2,-1,0,1,2,3,4,从中任意抽取一张卡片,则所抽卡片上数字的绝对值不大于2的概率是_______.
查看答案和解析>>
科目:初中数学 来源:2015届江苏省苏州市相城区八年级下学期期末考试数学试卷(解析版) 题型:解答题
某报社为了解苏州市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
请结合统计图表,回答下列问题.

(1)本次参与调查的市民共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请将图1的条形统计图补充完整;
(4)根据调查结果.学校准备开展关于雾霾知识竞赛,某班要从小明和小刚中选一人参加,现设计了如下游戏来确定:在一个不透明的袋中装有2个红球和3个白球,它们除了颜色外都相同,小明先从袋中随机摸出一个球,小刚再从剩下的四个球中随机摸出一个球,若摸出的两个球颜色相同,则小明去;否则小刚去.现在,小明同学摸出了一个白球,则小明参加竞赛的概率为多少?
查看答案和解析>>
科目:初中数学 来源:2015届江苏省盐城市东台市八年级下学期第一次月考数学试卷(解析版) 题型:选择题
下列性质中,平行四边形具有而非平行四边形不具有的是( )
A.内角和为360° B.外角和为360°
C.对角线互相平分 D.对角互补 ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com