
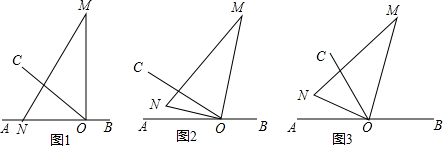
分析 (1)根据∠AOC=30°、OM恰好平分∠BOC知∠BOM=75°,进而可知旋转的度数,结合旋转速度可得时间t;
(2)根据图形和题意得出∠AON+∠BOM=90°,∠CON+∠COM=90°,再根据∠BOM=∠COM,即可得出ON平分∠AOC;
(3)根据图形和题意得出∠AON+∠BOM=90°,∠CON=∠COM=45°,再根据转动速度从而得出答案;
(4)分别根据转动速度关系和OC平分∠MOB画图即可.
解答 解:(1)∵∠AON+∠BOM=90°,∠COM=∠MOB,
∵∠AOC=30°,
∴∠BOC=2∠COM=150°,
∴∠COM=75°,
∴∠CON=15°,
∴∠AON=∠AOC-∠CON=30°-15°=15°,
解得:t=15°÷3°=5秒;
(2)是,理由如下:
∵∠CON=15°,∠AON=15°,
∴ON平分∠AOC;
(3)5秒时OC平分∠MON,理由如下:
∵∠AON+∠BOM=90°,∠CON=∠COM,
∵∠MON=90°,
∴∠CON=∠COM=45°,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
设∠AON为3t,∠AOC为30°+6t,
∵∠AOC-∠AON=45°,
可得:6t-3t=15°,
解得:t=5秒;
(4)OC平分∠MOB
∵∠AON+∠BOM=90°,∠BOC=∠COM,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
设∠AON为3t,∠AOC为30°+6t,
∴∠COM为$\frac{1}{2}$(90°-3t),
∵∠BOM+∠AON=90°,
可得:180°-(30°+6t)=$\frac{1}{2}$(90°-3t),
解得:t=$\frac{70}{3}$秒;
如图: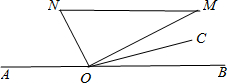
点评 此题考查了角的计算,关键是应该认真审题并仔细观察图形,找到各个量之间的关系求出角的度数是解题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源:2017届云南省普洱市九年级学业水平测试模拟考试(一)数学试卷(解析版) 题型:单选题
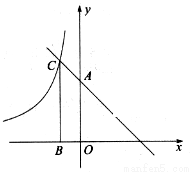
如图,直线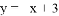 与
与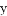 轴交于点A,与反比例函数
轴交于点A,与反比例函数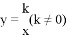 的图像交于点C,过点C作CB⊥
的图像交于点C,过点C作CB⊥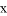 轴于点B,AO=3BO,则反比例函数的解析式为( )
轴于点B,AO=3BO,则反比例函数的解析式为( )
A. 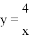 B.
B. 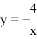 C.
C. 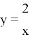 D.
D. 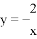
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
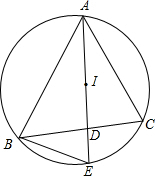 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
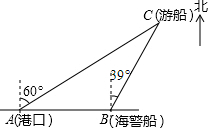 如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)
如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com